ما هي مساحة الشكل المركب

هي تكون منطقة ذات شكل معقد يعتمد ذلك على طريقة تقسيم الشكل المركب لـ أقرب أشكال هندسية بسيطة مثل المربع والمثلث والدائرة ، وفي هذه المقالة سنتحدث عن الأشكال المركبة بالتفصيل وسنشرح طريقة حسابها في مراحل مفصلة مساحة هذه الأشكال.

ما هي الاشكال المركبة

الأشكال المركبة (بالإنجليزية: Compound Figures) هي أشكال هندسية معقدة نسبيًا مقارنة بالأشكال الهندسية العادية ؛ حيث تحتوي الأشكال المركبة عادةً على مربعات ومثلثات ومستطيلات ودوائر ، وفي بعض الأشكال المركبة قد تحتوي على أشكال غير منتظمة وفي الحقيقة كلما كان الشكل أكبر ، كلما كان من الصعب على المركب حساب مساحته أو محيطه ، وبالتالي الشكل المعقد والمساحة والمحيط لتسهيل التعامل معها رياضيًا من حيث الأشكال البسيطة نسبيًا. في بعض الحالات ، يتم استعمال مستوى ديكاتور لحساب مساحة هذه الأشكال بالرغم من أن بعض هذه الأشكال يجب أن تستخدم قوانين التكامل. لحساب مساحتها أو محيطها ، وعادة ما يتم تقسيم الشكل المركب لـ الأشكال الأساسية التالية:

• مربعات.
• المستطيلات.
• الدوائر.
• مثلثات.
• شبه منحرف.
• الباستيل (الإنجليزية: معين).
• الفنانين.
• السداسيات.
• أشكال بيضاوية.

أنظر أيضا:

منطقة ذات شكل معقد

يمكن حساب مساحة الشكل المركب بتقسيم الشكل المركب لـ أشكال هندسية بسيطة مثل المربع والمثلث والدائرة ، ثم يتم حساب مساحة هذه الأشكال بشكل منفصل ، ثم مساحة هذه الأشكال يتم دمجها لمحيط الشكل ، لمعرفة مساحة مركب الشكل الكامل المركب ، لذلك طريقة الحساب لجمع أطوال أضلاع الشكل ، وإذا كانت هناك دوائر ، يتم حساب محيطها بشكل منفصل ، ثم جنبًا لـ جنب مع المحيط بأكمله ، وهنا بعض من أهم القوانين لحساب مساحة الأشكال الهندسية الأساسية والبسيطة:

• قانون مساحة ومحيط المربع:

مساحة المربع = طول الضلع²
محيط المربع = طول الضلع × 4

• قانون مساحة ومحيط المستطيل:

مساحة المستطيل = الطول × العرض
محيط المستطيل = 2 × (الطول + العرض)

• قانون مساحة المثلث والمحيط:

مساحة المثلث = ½ x القاعدة x الارتفاع
محيط المثلث = طول الضلع الأول + طول الضلع الثاني + طول الضلع الثالث

• قانون مساحة ومحيط متوازي الأضلاع:

مساحة متوازي الأضلاع = القاعدة × الارتفاع
محيط متوازي الأضلاع = طول الضلع الأول + طول الضلع الثاني + طول الضلع الثالث + طول الضلع الرابع

• قانون مساحة الدائرة ومحيطها:

مساحة الدائرة = نصف القطر ² x
المحيط = 2 × Π × نصف القطر

• قانون مساحة ومحيط شبه منحرف:

= ½ x (القاعدة الأولى + القاعدة الثانية) x الارتفاع
محيط الرقعة = طول الضلع الأول + طول الضلع الثاني + طول الضلع الثالث + طول الضلع الرابع

• قانون مساحة ومحيط الماس:

مساحة المعين = ½ x القطر الأول x القطر الثاني
محيط المعين = طول الضلع الأول + طول الضلع الثاني + طول الضلع الثالث + طول الضلع الرابع

أنظر أيضا:

أمثلة لحساب مساحة الأشكال المعقدة

فيما يلي بعض الأمثلة حول طريقة حساب مساحة الأشكال المركبة:

المثال الأول

احسب مساحة الشكل المركب في الصور أدناه:

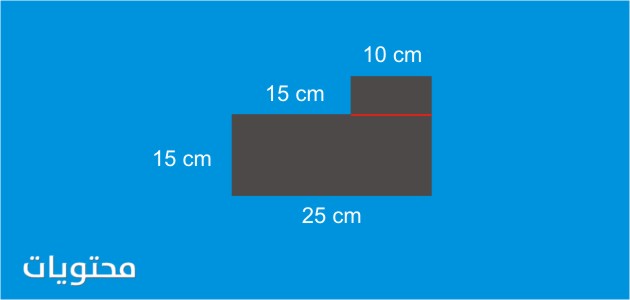
في الشكل أعلاه ، نرى أن الشكل المركب به مستطيلين فوق بعضهما البعض ، وبالتالي يمكن تقسيم الشكل المركب لـ جزأين ، ثم حساب مساحة المستطيل الأول ، وهي 25. احسب مساحة المستطيل الصغير الثاني ، طوله سم وعرضه 15 سم ، ثم طوله 10 سم وعرضه 15 سم ، ثم نجمع المساحتين معًا لتشكيل مساحة الشكل المركب ، وطريقة الحل كالتالي:

• مساحة المستطيل الأول:
  مساحة المستطيل الأول = الطول × العرض
  مساحة المستطيل الأول = 25 × 15
  مساحة المستطيل الأول = 375 سنتيمترا مربعا
• مساحة المستطيل الثاني:
  مساحة المستطيل الثاني = الطول × العرض
  مساحة المستطيل الأول = 10 × 15
  مساحة المستطيل الأول = 150 سم مربع
• منطقة ذات شكل معقد:
  مساحة الشكل المركب = مساحة المستطيل الأول + مساحة المستطيل الثاني
  مساحة الشكل المركب = 375 + 150
  مساحة الشكل المركب = 525 سم مربع

المثال الثاني

احسب مساحة الشكل المركب في الصور أدناه:

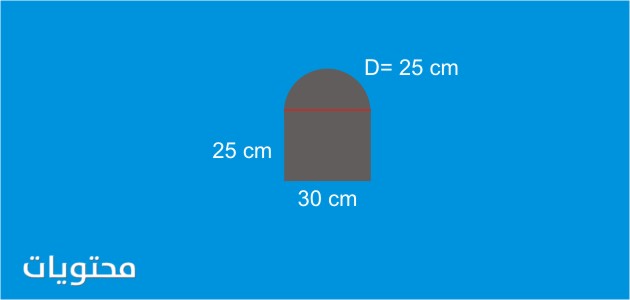
في الشكل أعلاه ، نلاحظ أن الشكل المركب هو مستطيل به نصف دائرة بحيث يمكن تقسيم الشكل المركب لـ قسمين ، ثم نحسب مساحة المستطيل بطول 30 سم. العرض 25 سم ، ثم احسب مساحة نصف الدائرة بقطر 25 سم ، ثم نجمع المنطقتين لتشكيل مساحة الشكل المركب ، وطريقة الحل على النحو التالي:

• منطقة مستطيلة:
  مساحة المستطيل = الطول × العرض
  مساحة المستطيل = 30 × 25
  مساحة المستطيل = 750 سنتيمترا مربعا
• منطقة نصف دائرة:
  مساحة الدائرة = نصف القطر ² x
  مساحة الدائرة = ²12.5 × Π
  مساحة الدائرة = 490.265 سنتيمترًا مربعًا
  مساحة نصف الدائرة = مساحة الدائرة 2
  مساحة نصف الدائرة = 490.265 2
  مساحة نصف الدائرة = 245.3 سم مربع
• منطقة ذات شكل معقد:
  مساحة الشكل المركب = مساحة المستطيل + مساحة نصف الدائرة
  مساحة الشكل المركب = 750 + 245.3
  مساحة الشكل المركب = 995.3 سم مربع

المثال الثالث

احسب مساحة الشكل المركب في الصور أدناه:

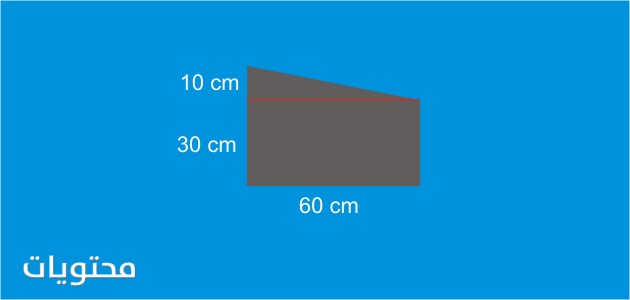
في الشكل أعلاه ، لاحظنا أن الشكل المركب عبارة عن مستطيل ومثلث قائم الزاوية عليه ، وبالتالي يمكن تقسيم الشكل المركب لـ قسمين ثم حساب مساحة المستطيل. يبلغ طولها 60 سم وعرضها 30 سم ، ثم احسب مساحة المثلث المدير بطول 60 سم وارتفاعه 10 سم ، ثم جمع المنطقتين ، يكون الشكل المركب وطريقة الحل كما يلي :

• منطقة مستطيلة:
  مساحة المستطيل = الطول × العرض
  مساحة المستطيل = 60 × 30
  مساحة المستطيل = 1800 سم مربع
• مساحة المثلث الأيمن:
  مساحة المثلث المدير = ½ x القاعدة x الارتفاع
  مساحة المثلث المدير = ½ × 60 × 10
  مساحة المثلث المدير = 300 سم مربع
• منطقة ذات شكل معقد:
  مساحة الشكل المركب = مساحة المستطيل + مساحة المثلث الأيمن
  مساحة الشكل المركب = 1800 + 300
  مساحة الشكل المركب = 2100 سم مربع

المثال الرابع

احسب مساحة الشكل المركب في الصور أدناه:

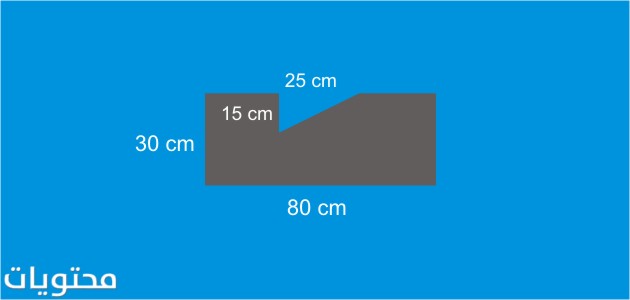
في الشكل أعلاه ، لاحظنا أن الشكل المركب عبارة عن مستطيل يُستخرج منه مثلث قائم الزاوية ، وبالتالي يمكن تقسيم الشكل المركب لـ قسمين ، ثم حساب مساحة المستطيل. الطول 80 سم والعرض 30 سم ، ثم احسب مساحة المثلث المدير بطول 25 سم وارتفاعه 15 سم ، ثم نطرح المنطقتين معًا لنحصل على مساحته. الشكل المركب وطريقة الحل هي كما يلي:

• منطقة مستطيلة:
  مساحة المستطيل = الطول × العرض
  مساحة المستطيل = 80 × 30
  مساحة المستطيل = 2400 سنتيمترا مربعا
• مساحة المثلث الأيمن:
  مساحة المثلث المدير = ½ x القاعدة x الارتفاع
  مساحة المثلث المدير = ½ × 25 × 15
  مساحة المثلث المدير = 187.5 سم مربع
• منطقة ذات شكل معقد:
  مساحة الشكل المركب = مساحة المستطيل – مساحة المثلث الأيمن
  مساحة الشكل المركب = 2400 – 187.5
  مساحة الشكل المركب = 2212.5 سم مربع

في انتهاء هذه المقالة ، سنعرف طريقة الحساب منطقة ذات شكل معقد في مراحل تفصيلية ، شرحنا أيضًا ماهية الشكل المركب وتحدثنا عن الكثير من الأمثلة المهمة لكيفية حساب مساحة الأشكال المركبة.

المراجع

1. doodlemaths.com ، 28/1/2021

2. sciencing.com ، 28/1/2021