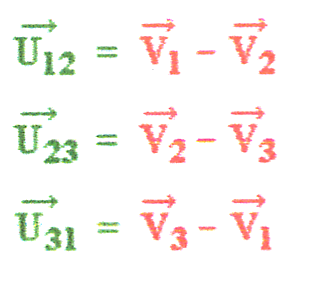يمكنك تنزيل الموضوع كاملاً من الرابط أعلاه أو قراءة النسخة المعدلة من الأسفل.
شهادة أستاذ |
الدوائر الكهربائية في التيار المتردد
تليين لقد رأينا سابقًا أنه من الممكن توليد قوة دافعة كهربائية عندما نغير كمية التدفق عبر ملف:
الملف يدور بسرعة الزاوية ث يحدث التغيير في الفضاء بواسطة مغناطيس دائم س اي التغيير في التدفق Φإذن تغيير في المجال ب إذا تم إحداث قوة تحفيزية كهربائية لـ يمكن قياسه بواسطة الفولتميتر. |
دوران المغناطيس بسرعة زاويةث مع ملف ثابت يحدث تغيير في التدفق Φ إذن تغيير في المجال ب إذا تم إحداث قوة تحفيزية كهربائية لـ يمكن قياسه بواسطة الفولتميتر. |
بعد استكشاف التيار المباشر ، أدركنا أن هناك نوعًا ثانيًا من التيار وهو تيار متغير لأن التدفق متغير. .
الثاني- أنواع الإشارات الكهربائية : تنقسم الإشارات لـ قسمين:
الإشارة المتجددة (الحالية): هي إشارة لا تتغير بمرور الوقت ويتم تحديدها عبر قيمتها (الشكل 1).
التيارات المقدرة : تُصنف التيارات كماًا لاتجاه دورانها:
ج) – التدفقات الدورية : تيار متغير يسمى دوري ، والذي يأخذ نفس القيمة في الفترتين T1 و t1 + nT (يوجد تكرار لنفس الشكل خلال فترة محددة T) حيث:
t1: لحظة محددة
n: العدد الطبيعي
T: هو مجال زمني يسمى periode ووحدته (وحداته) الثانية.
مثال في الجزائر ، التوزيع الحالي دوري في الشبكة والدورة T = 20ms.
وحدة التردد هي هرتز (هرتز).
مثال : شبكة توزيع التيار الكهربائي في الجزائر توزع التيار على تردد f = 50Hz.
المقادير الكهربائية المميزة للإشارات : قيم الجهد u
يشار لـ القيم القصوى بواسطة Î ،
تعني القيم المشار إليها بـ Ī أو ،
القيم الفعالة أو الإنتاجية التي يشير إليها I ، U
أ) – ذات قيمة عظيمة : يمكن قياس القيمة القصوى للدالة u
ب) – متوسط القيمة : نظرًا لأن متوسط القوة الحالية للتيار المتغير يساوي كثافة التيار المستمر الذي يحمل نفس الكمية من الشحنة الكهربائية Q خلال نفس المدة الزمنية ، فيمكن تحديده عبر المقارنة مع التيار المستمر.
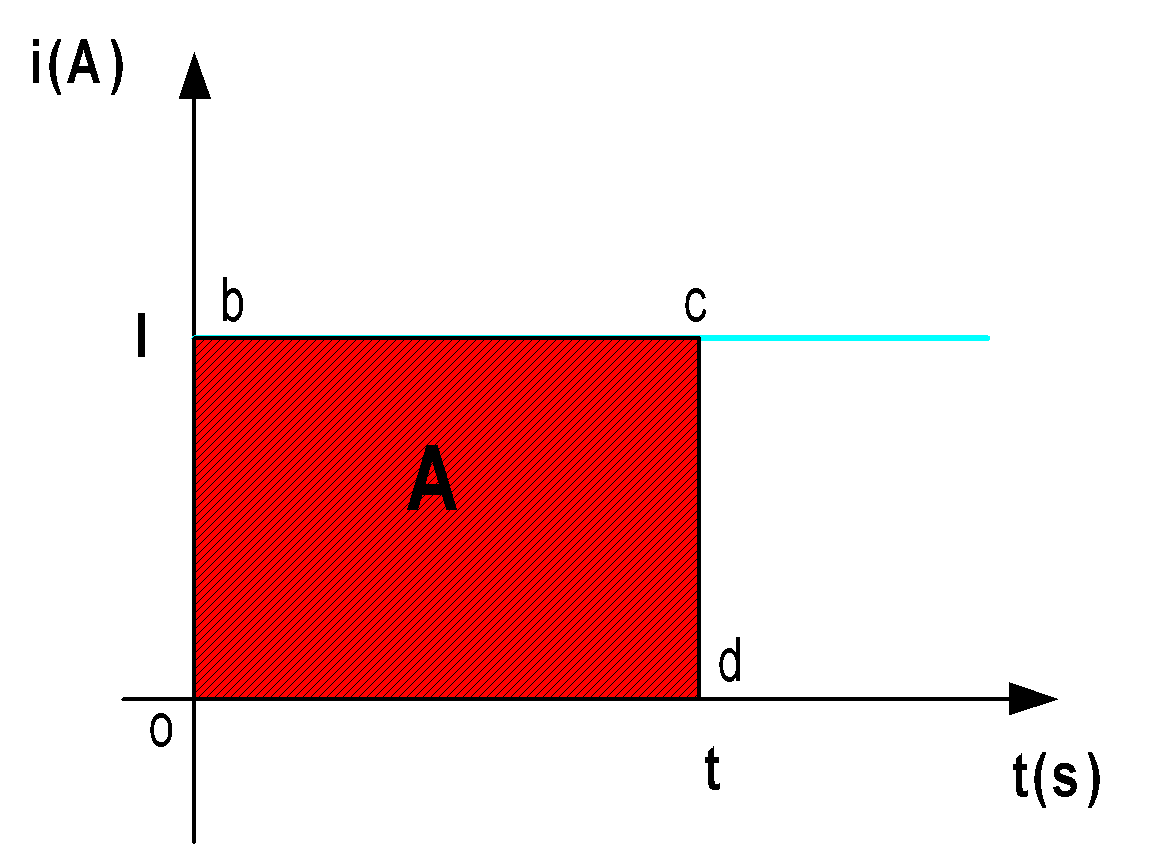
يمثل الشكل المقابل مقدارًا ثابتًا من التيار I. كمية الكهرباء س
خلال الوقت يتم تمثيل T obcd في المنطقة A من المستطيل.
إذن المنطقة أ = الشحنة الكهربائية Q.
دع “الشكل 5” تكون منطقة A2 ، obcd ، منطقة المستطيل.
التيار المتغير i
يمثل الحقل A2 كمية الكهرباء المحولة من محطة التيار المستمر I.
مساحة A1 = مساحة A2 ، أنا هي القيمة المتوسطة
للمتغير الحالي أنا (تي).
ملاحظات:
يتم تحديد متوسط ذات قيمة التيار الدوري على مدار فترة زمنية.
بالنسبة للتيار ثنائي الاتجاه ، يتم حساب المناطق التي تقع أسفل المحور الأفقي بشكل سلبي.
يعتبر التيار ذو القيمة المتوسطة للصفر متناوبًا ، أي أن مساحة القص الإيجابية تساوي منطقة القص السلبية.
يتم قياس متوسط ذات قيمة التيار المتغير باستخدام مقياس التيار الكهرومغناطيسي في وضع ثابت ، وتكون القراءة مباشرة.
اي
لحساب القيمة الفعالة للتيار i مع المنحنى i
لذلك أنا (تي) هو تيار متناوب.
القيمة الفعالة لـ (i
د) – التيار الجيبي المتناوب: نقول أن تيار المتغير الجيبي ، يجب أن يكون تعبيره:
هنا: i
أنا تسمى القيمة القصوى للتيار السعة أو وحدة السعة والسعة القصوى.
ω : النبضة أو السرعة الزاوية (راديان / ثانية) لتمديد الراديان في الثانية.
(ω ر + φ): الطور أو الصفحة اللحظية ، وهي زاوية تتغير بمرور الوقت ، الوحدة راديان (راد).
φ : المرحلة الأولية ، أي الزاوية عند t = 0s ووحدتها راديان.
-1 ≤ الخطيئة (ω t + φ) ≤ 1.
النبض والدوران والتردد:
تي: في ثوان
f: التردد بالهرتز
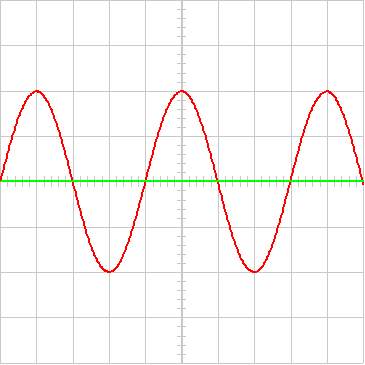
* متوسط القيمة : متوسط ذات قيمة التيار المتردد
جيبي صفر.
ذات قيمة فعالة : القيمة الفعالة للتيار المتردد الجيبي
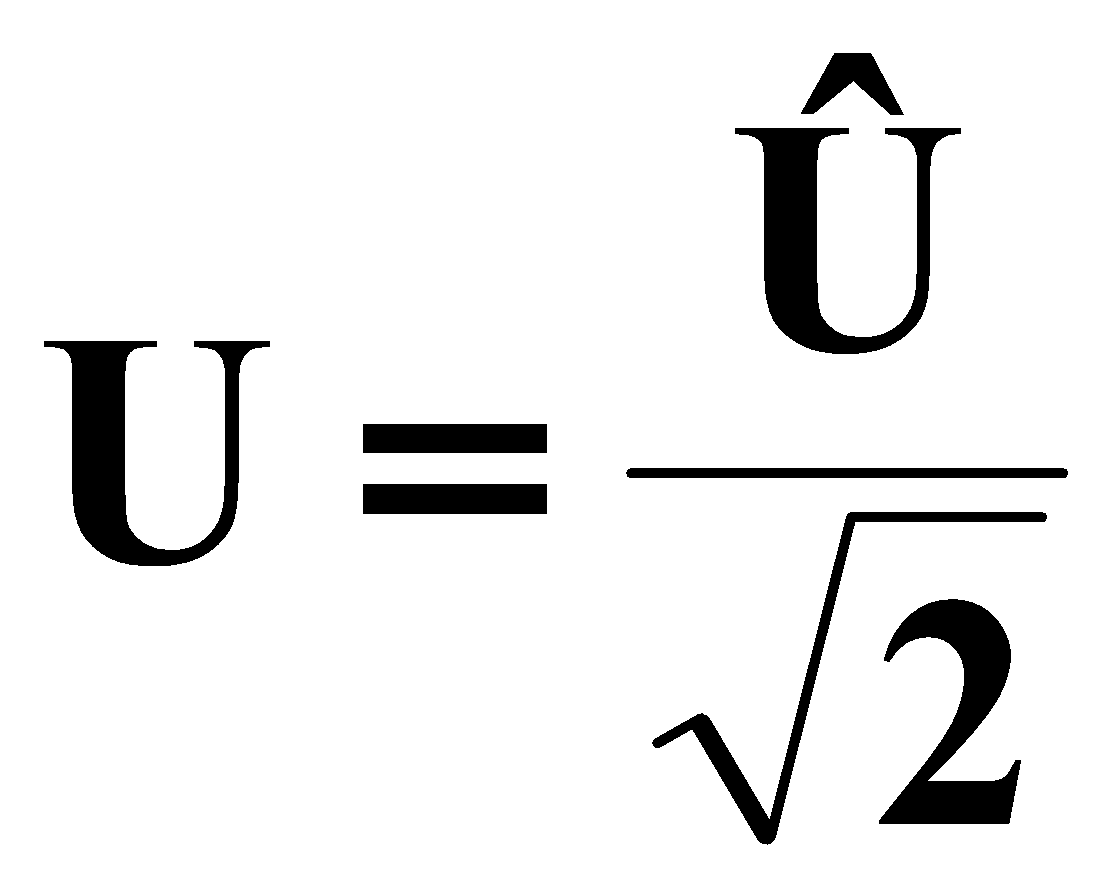
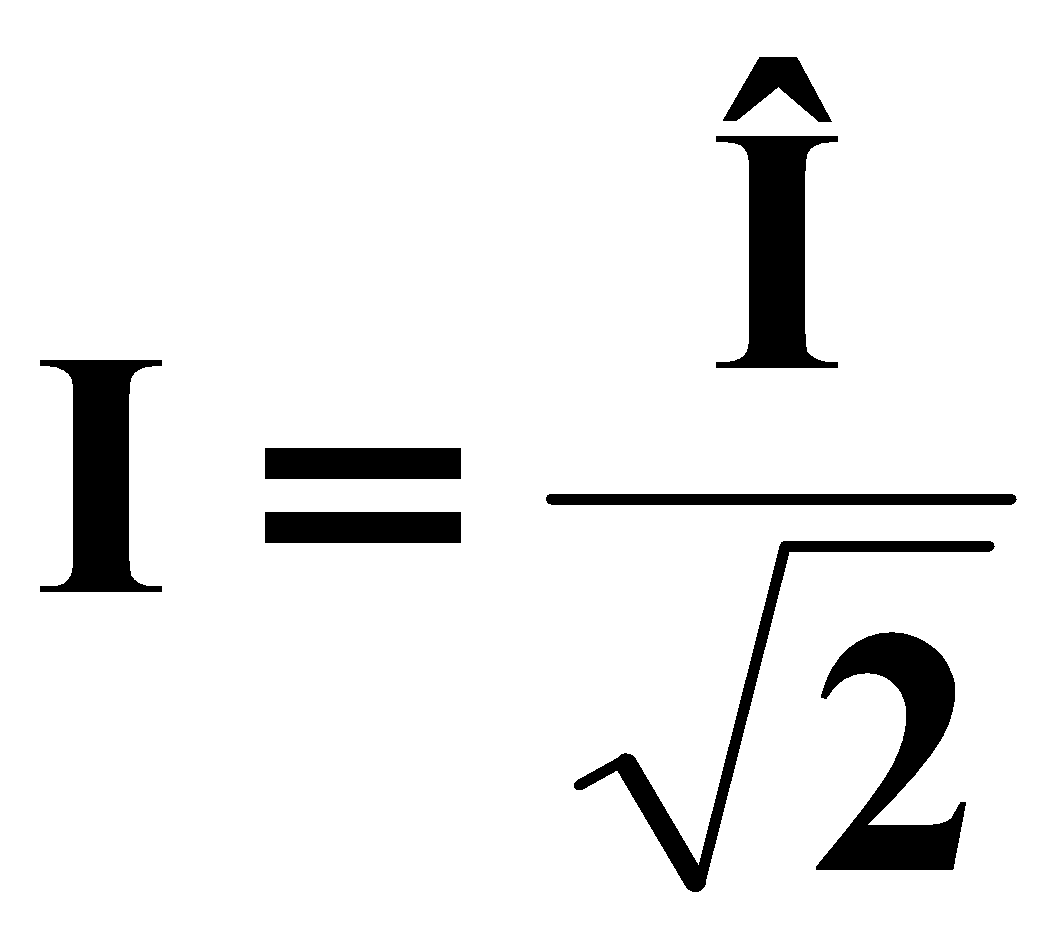
من الناحية المهمة ، يتم تعريف قيم u و i على أنها قيم فعالة ، لذلك نسمي الشبكة v 220 ، أي أن القيمة الفعالة تساوي 311.
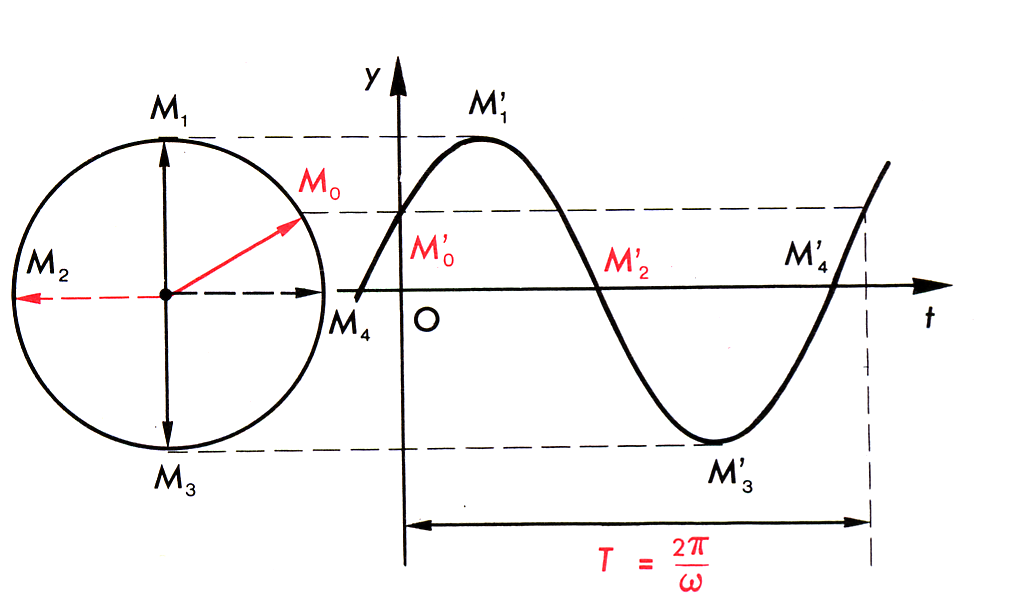
3- تمثيل فرينل :
إنها حركة من الوظائف الشعاعية لـ الوظائف الجيبية التي تسمح باستبدال وظيفة الجيب بحزمة هدفها:
مقارنة بين وظيفتين من وظائف الجيب بنفس التردد.
إضافة وظائف جيبية بنفس التردد.
* شعاع فرينل :
لكل حجم جيبي u
– شعاع OM الجدول إنها تساوي القيمة القصوى للتعبير الفنان: = Û || أوم || .
زاوية (ثور ، أوم0) الصفحة أو المرحلة الأولية ، أي الموضع M عند t = 0s M.0 إذن φ = (ox، oM0)
– تشكل الزاوية (ox، oM) الصفيحة أو الطور اللحظي ، أي موضع النقطة M في الوقت t.
(ox، oM) = (ox، oM0) + (أوم0، أوم) = ωt + φ
دع m يكون الإسقاط M على محور التصويت.
om = u
لذلك نقول أن الجهد الجيبي u

* دوران الشعاع والتمثيل الديكارتي:
(ش (ر) = Ûsin (t + φ
Û || = أوم ||
* المعاوقة ثنائية القطب سلبية وخطية:
الصمام الثنائي السلبي الخطي عبارة عن دائرة لا تحتوي على قوة دافعة كهربائية ، وأنماطها لها قيم ثابتة مثل المكثف C – الملف L – المقاومة R.
إذا قمنا بتغذية ثنائي القطب بجهد جيبي u
عندما يمثل Z الممانعة الحقيقية لثنائي القطب ووحدته أوم كمقاومة.
تشكل U و I قيمًا فعالة في التيار المتناوب والمقادير هي نفسها في التيار المباشر.
R ثابت ولكن Z يظل ثابتًا إذا لم يتغير التردد f.
وحدة Ω-واحد أو سيمنز.
قانون أوم للدوائر الكهربائية المختلفة :
مقاومة الصرفة R :
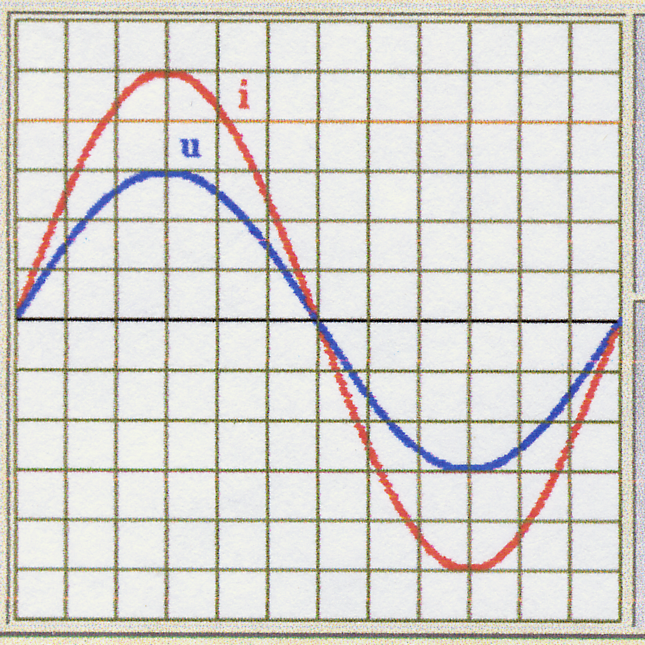
(ش (ر) = Ûsin (t + φ
التيار أنا والتوتر يتفقان على الصفحة
Z = R و φ = 0.
* و coa مثالية L:
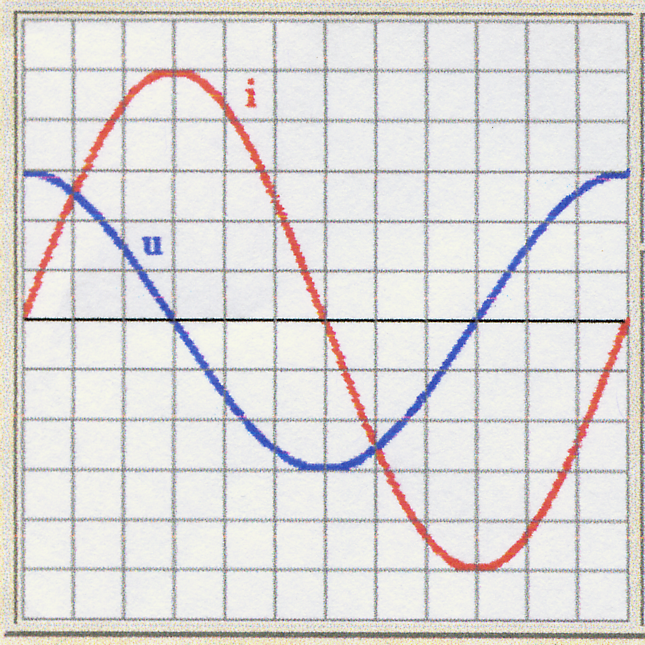
السلالة U في ترتيب أمامي فيما يتعلق بالتيار i.
Z = L ω و
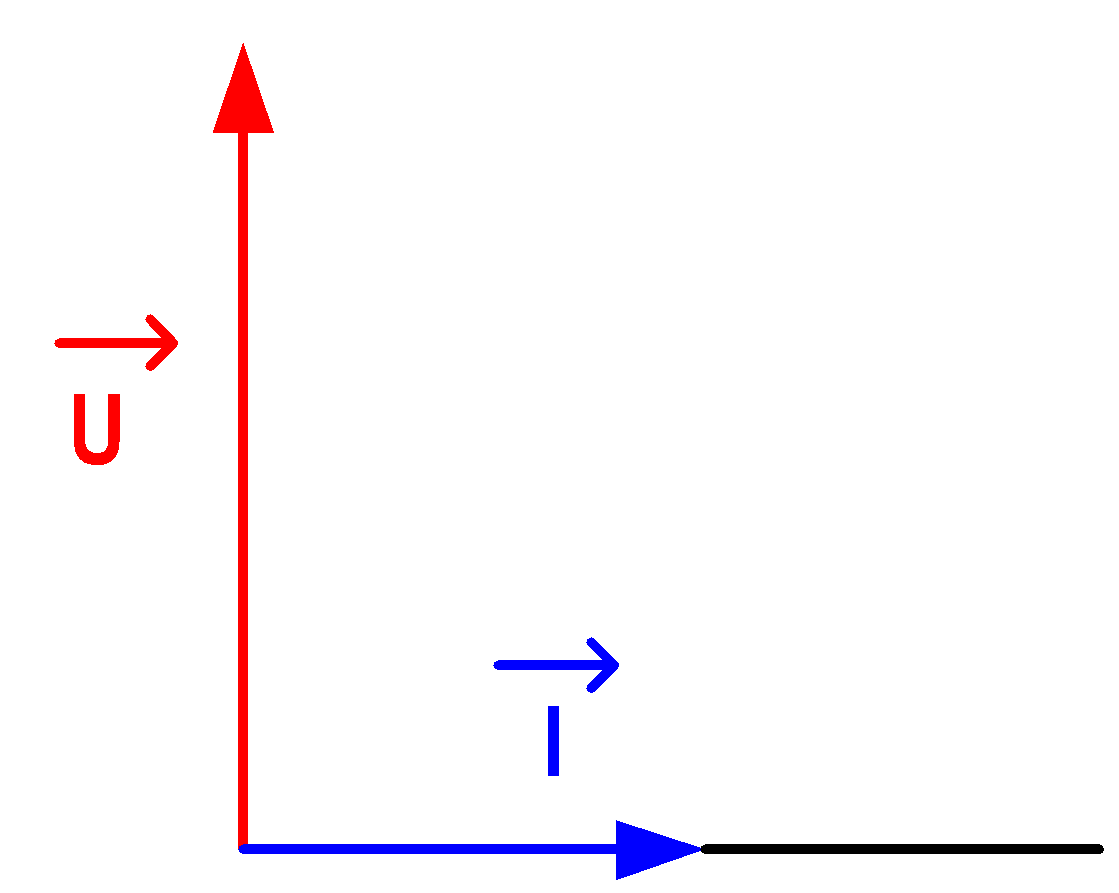
* كثيف أ:
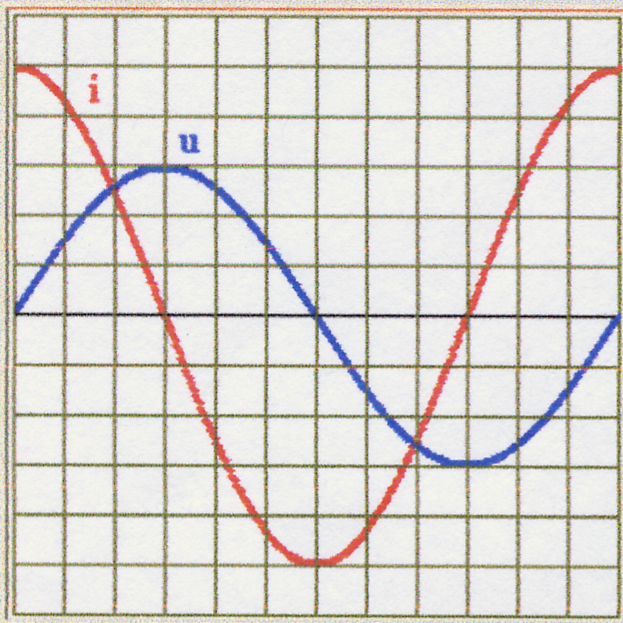
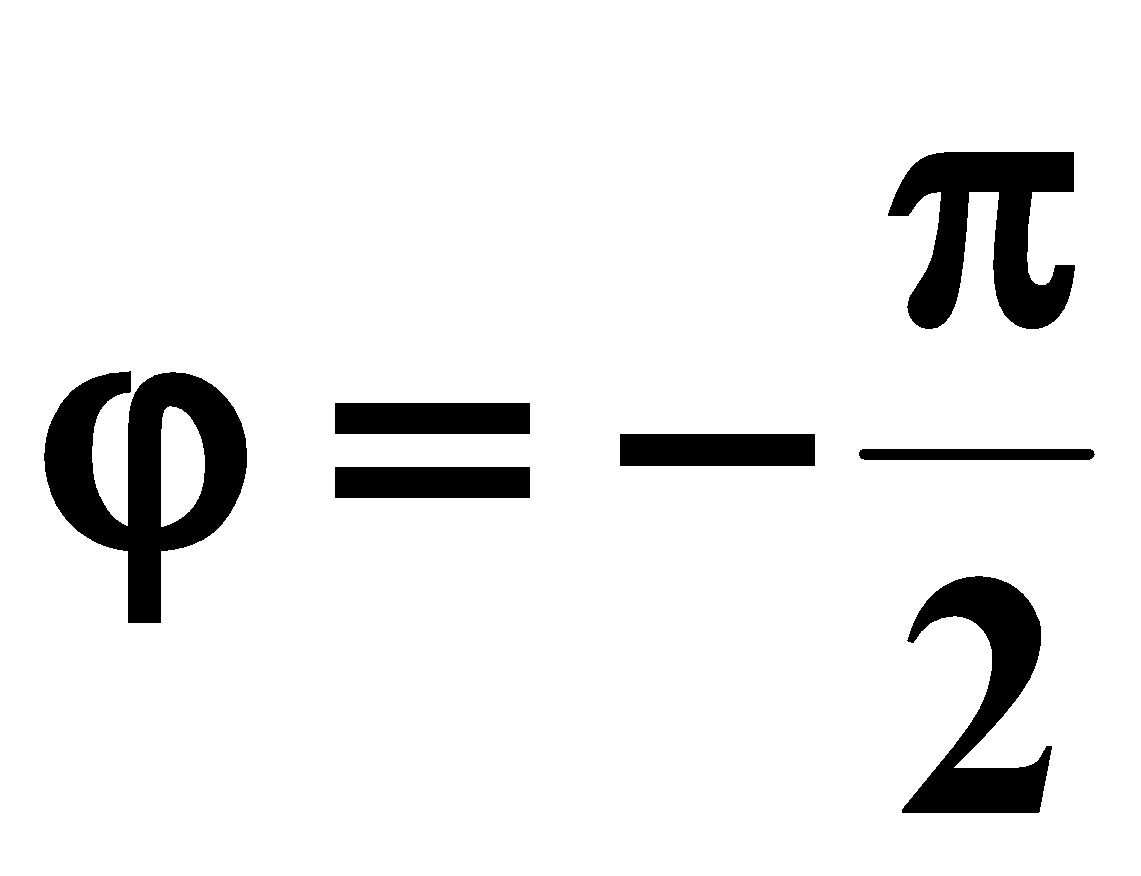
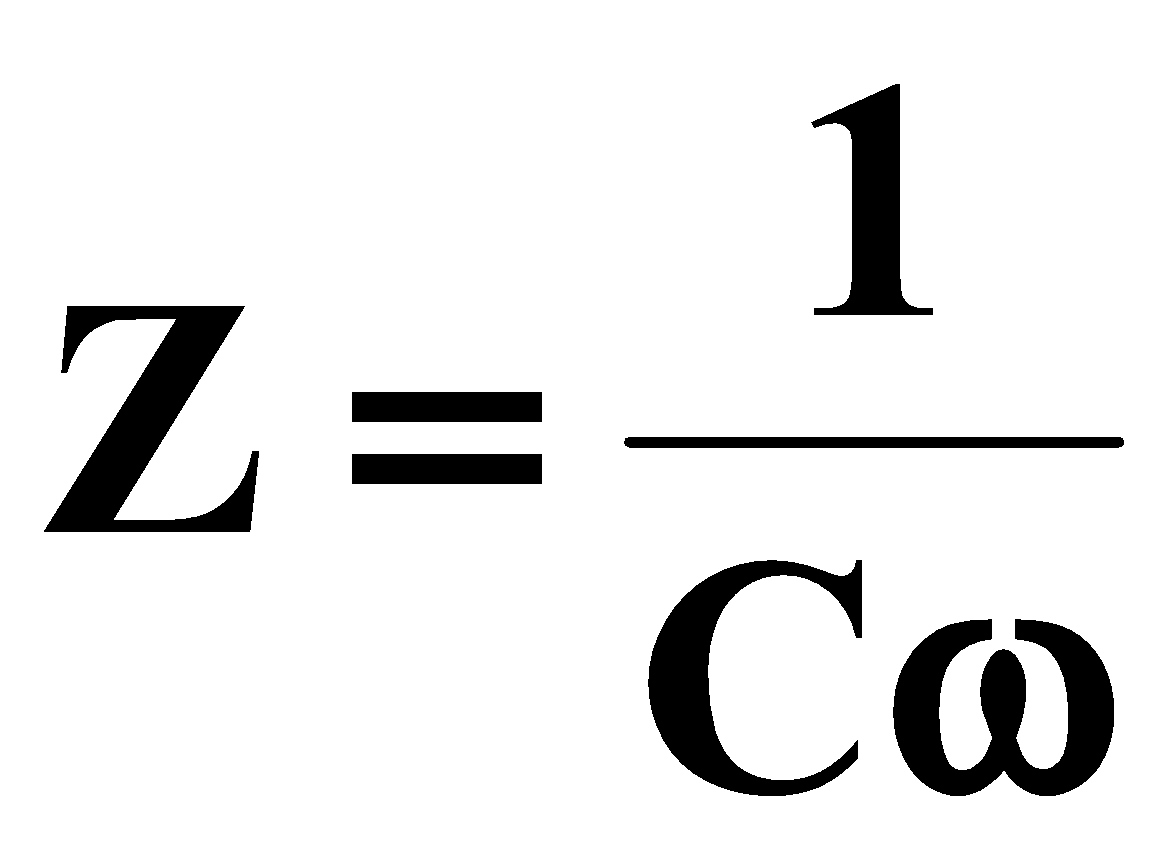
و
تمثيل فرينل : 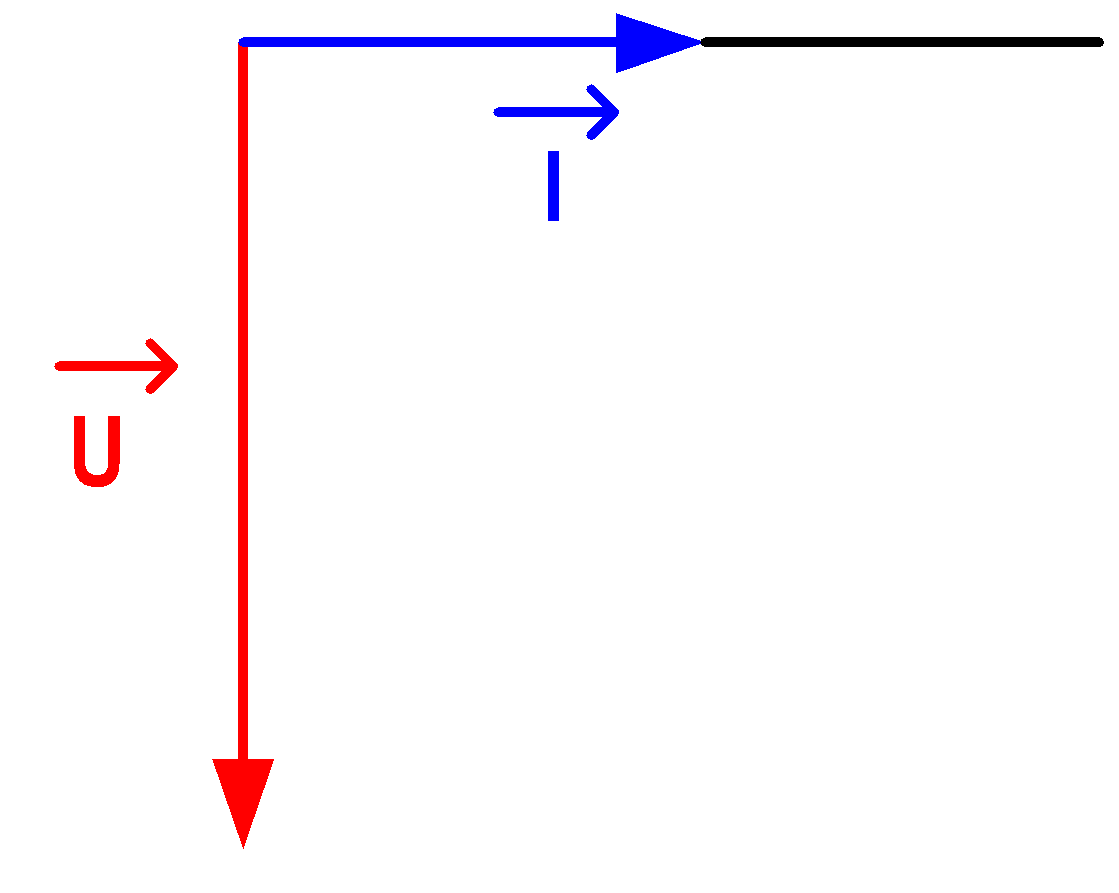
* لفائف المقاومات R و L على التوالي:
![]()
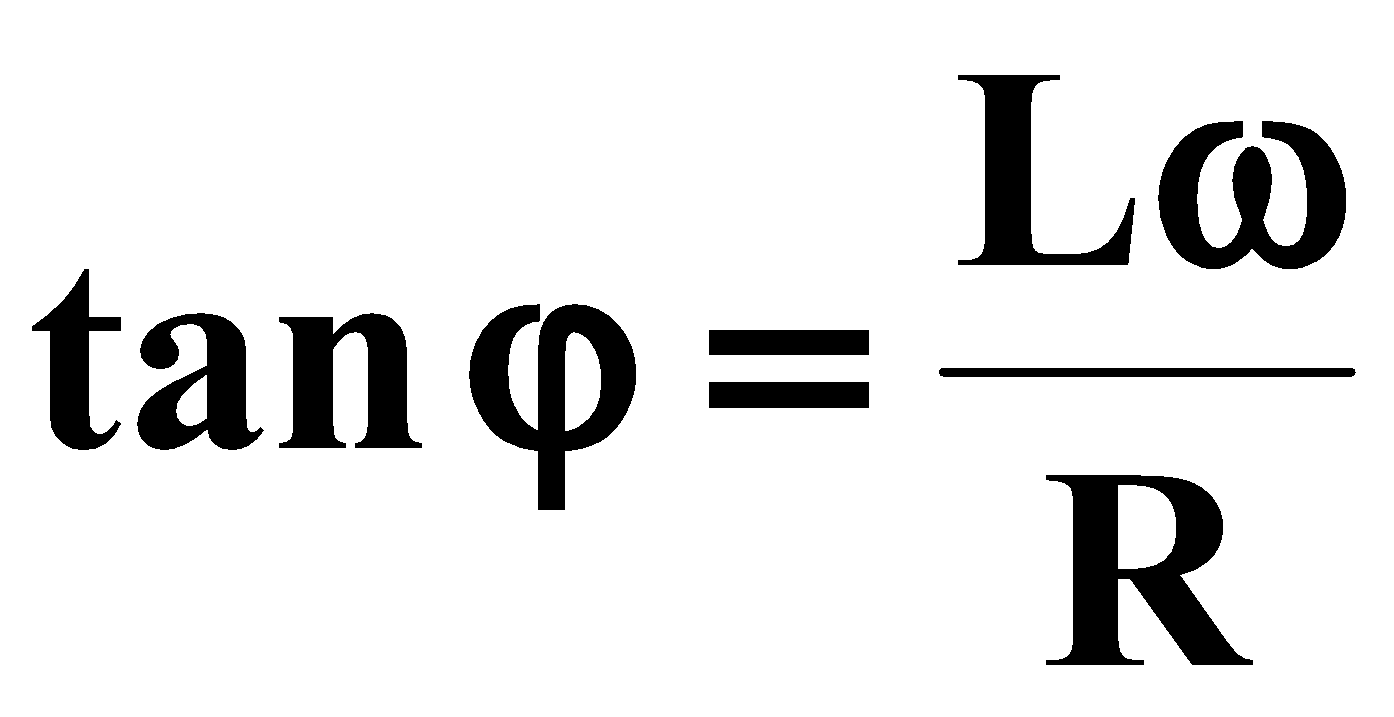
تمثيل فرينل :
* المقاومات R والملف L والمكثف C على التوالي:
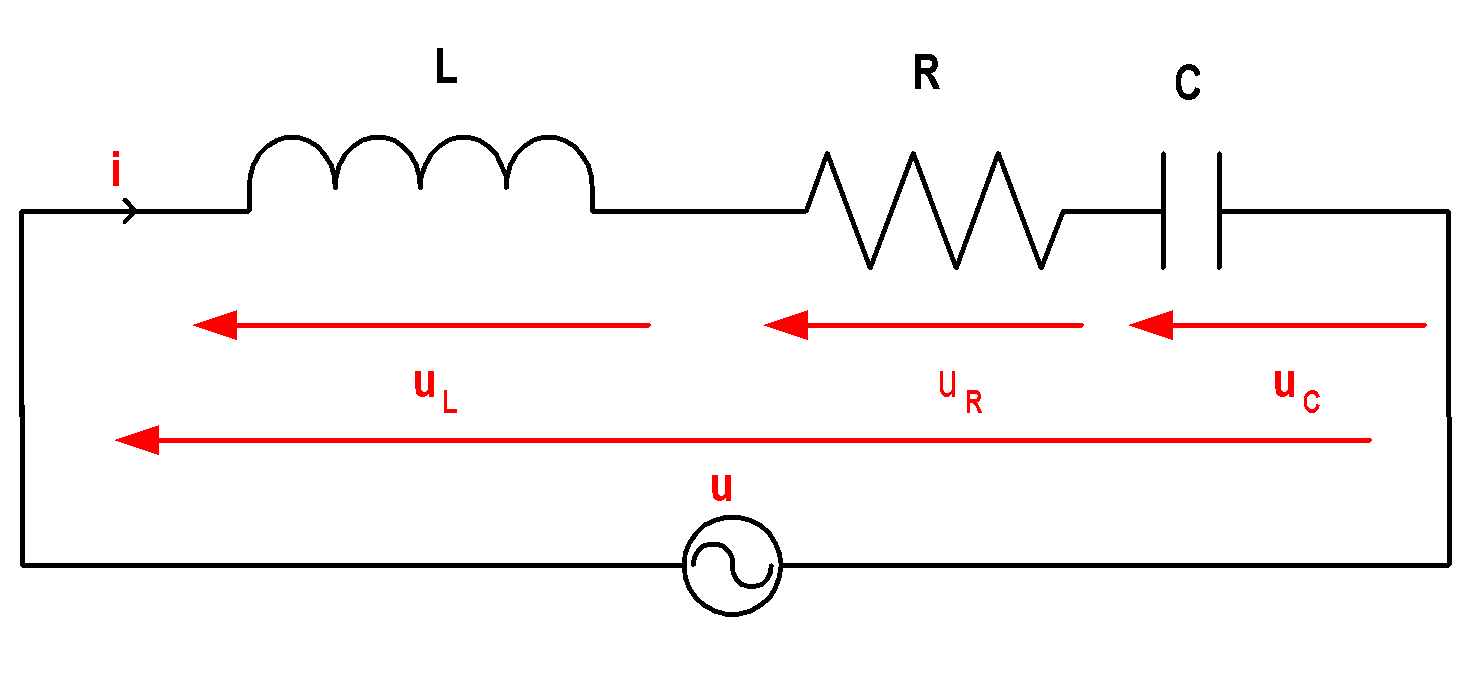
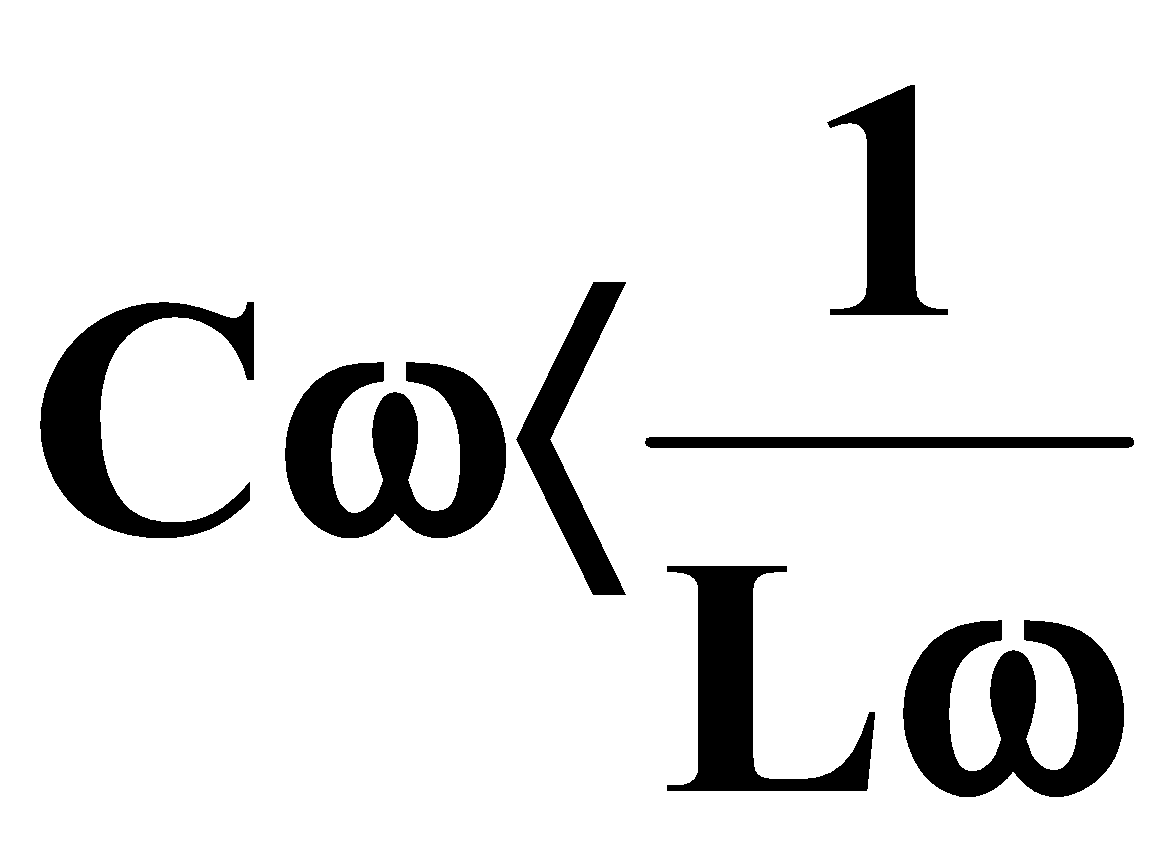
يتجاوز الفعل الفعلي للملف فعل المكثف (الدائرة الحثية)
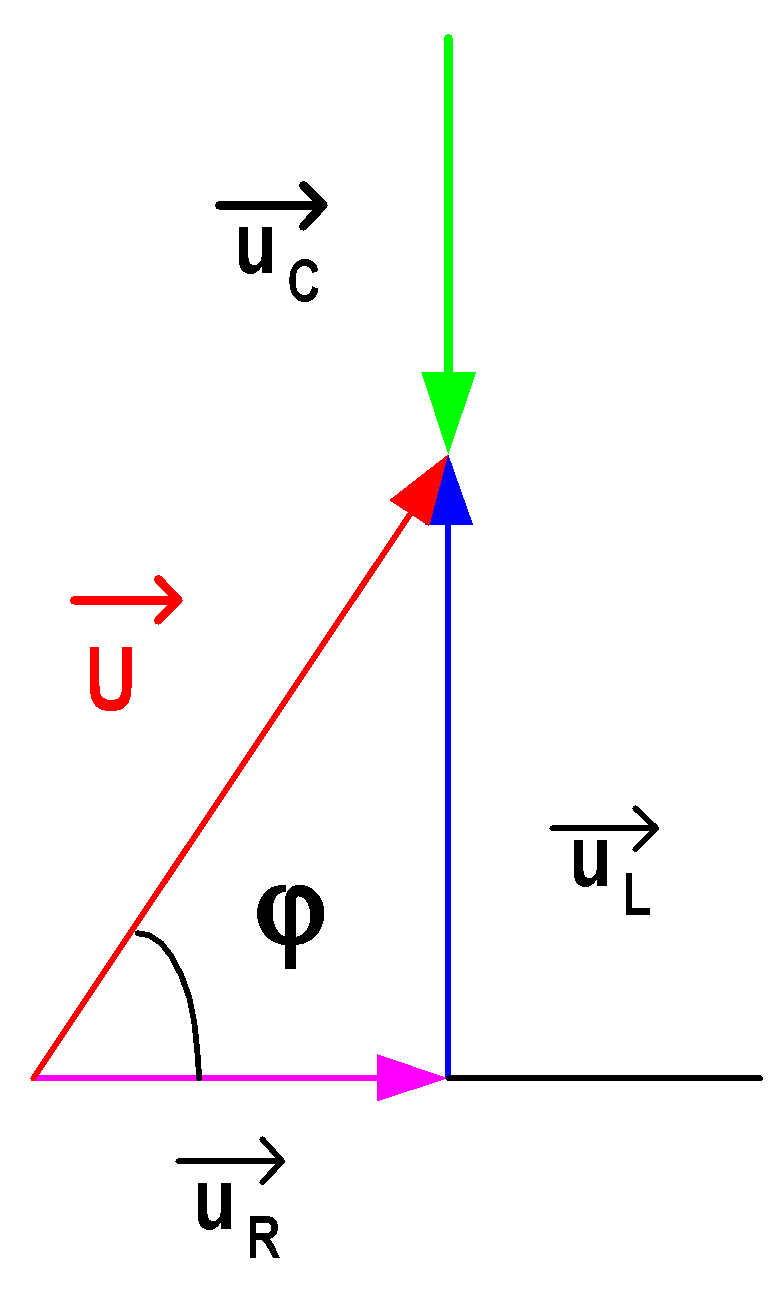
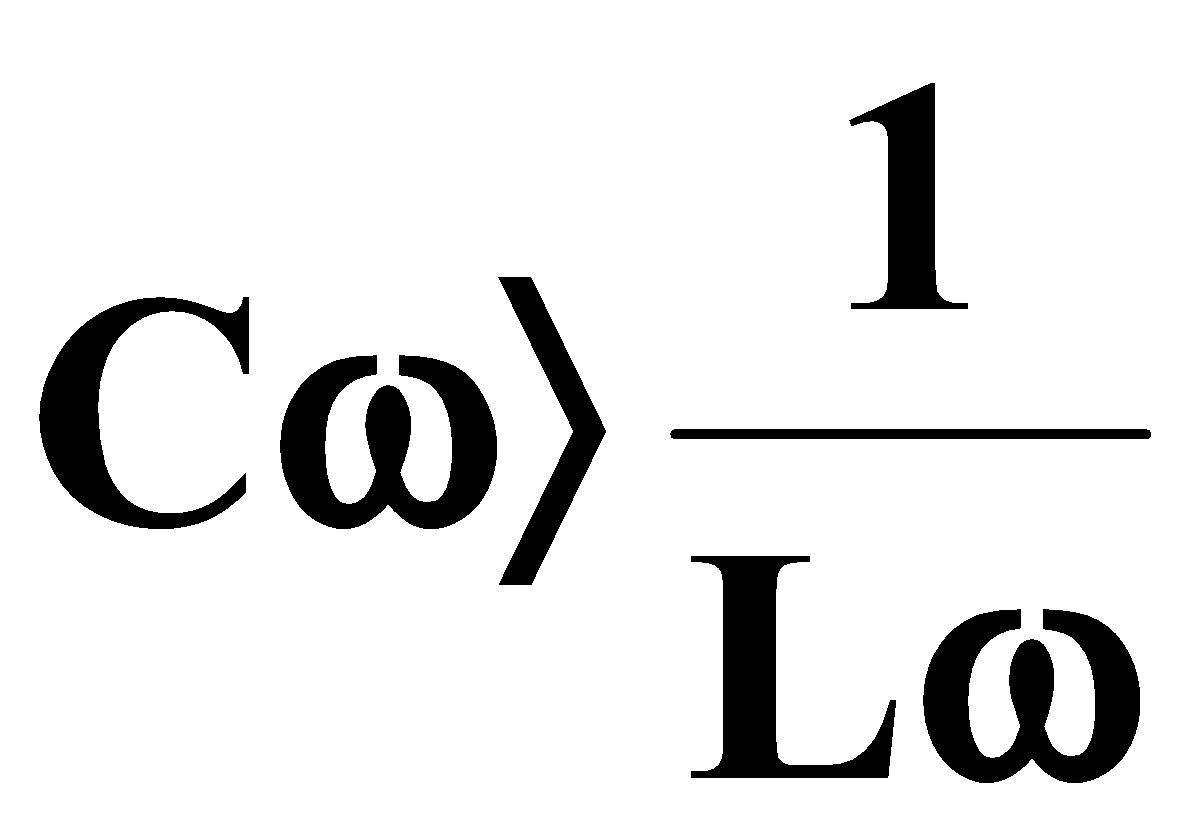
يسيطر الفعل المكثف على الفعل المكثف (الدائرة السعوية).
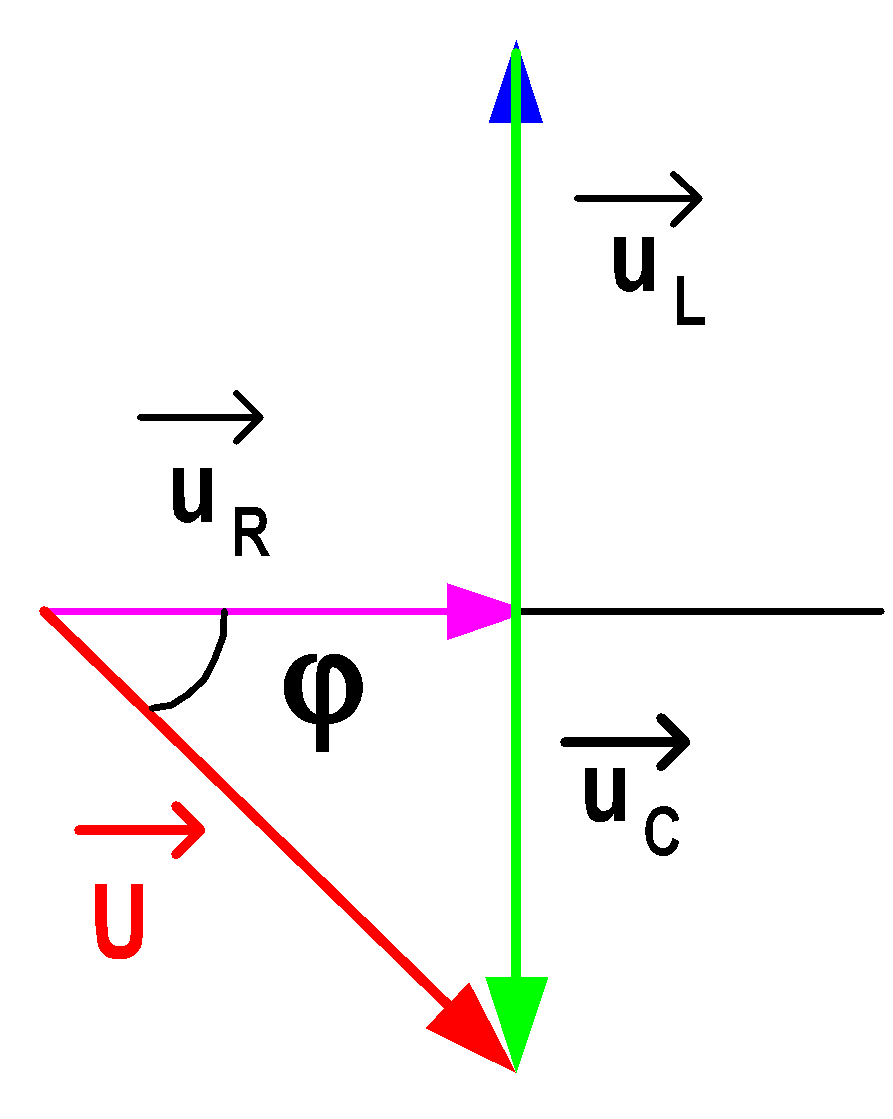
φ <0 span = "">
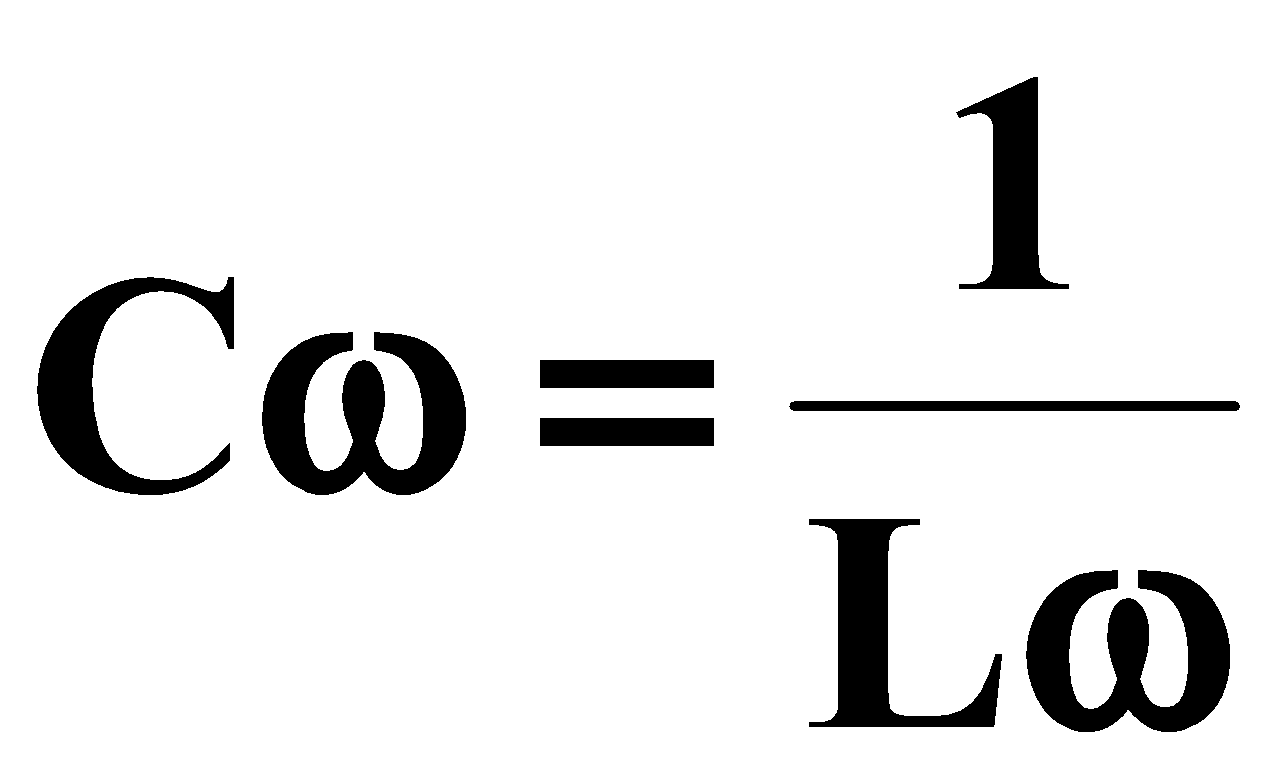
الفعل المكثف يساوي الفعل والقافية (حالة حساسة).
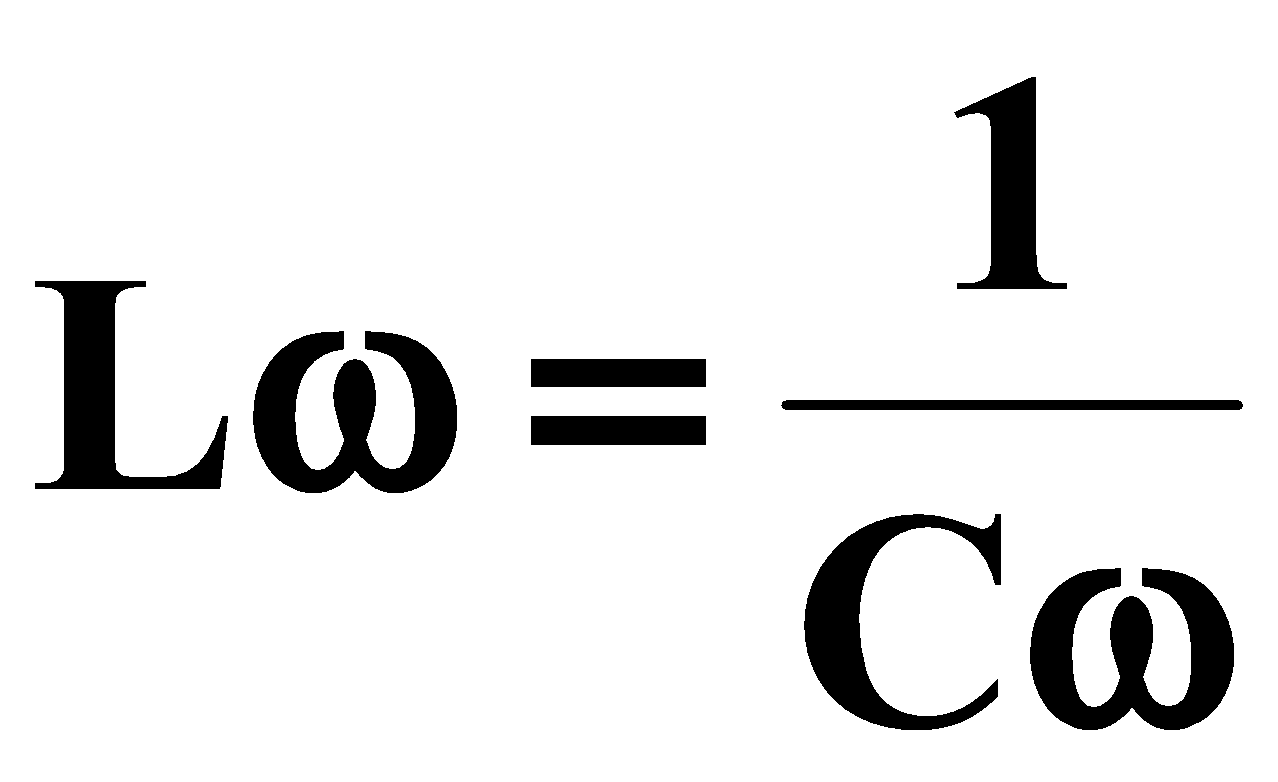
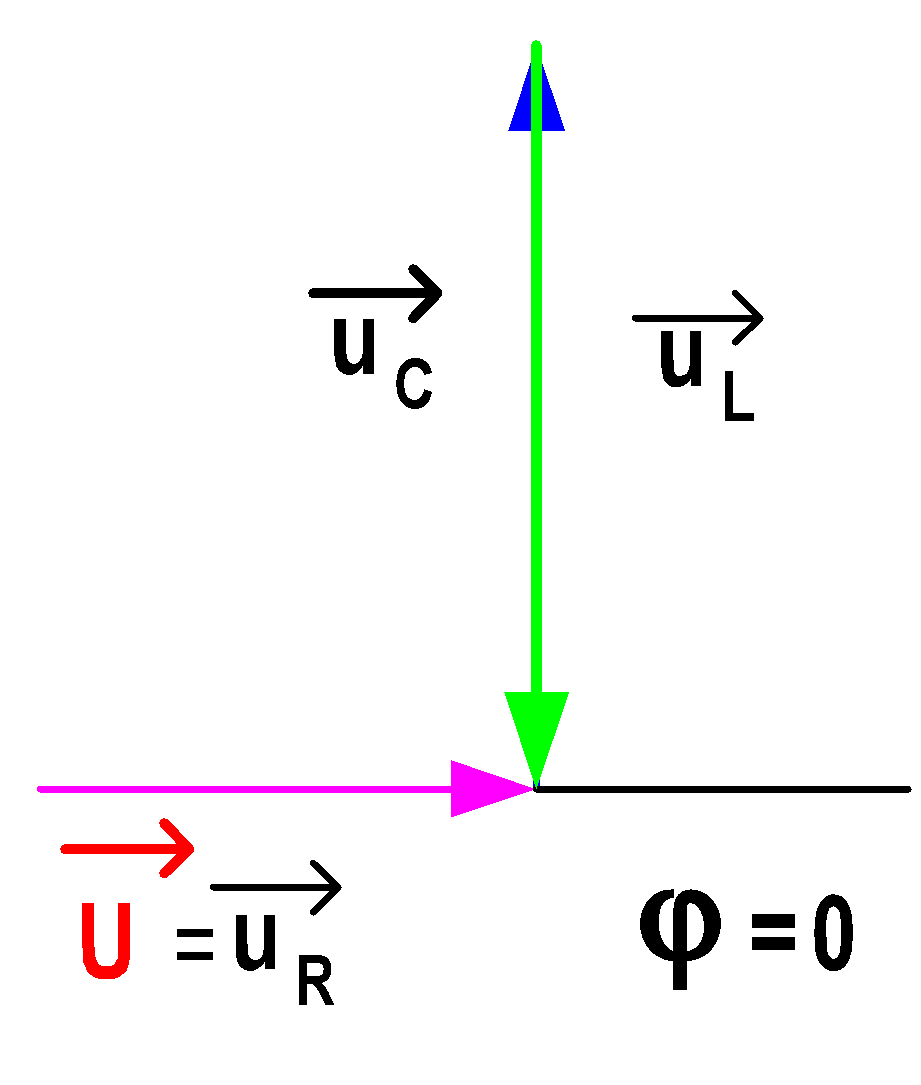
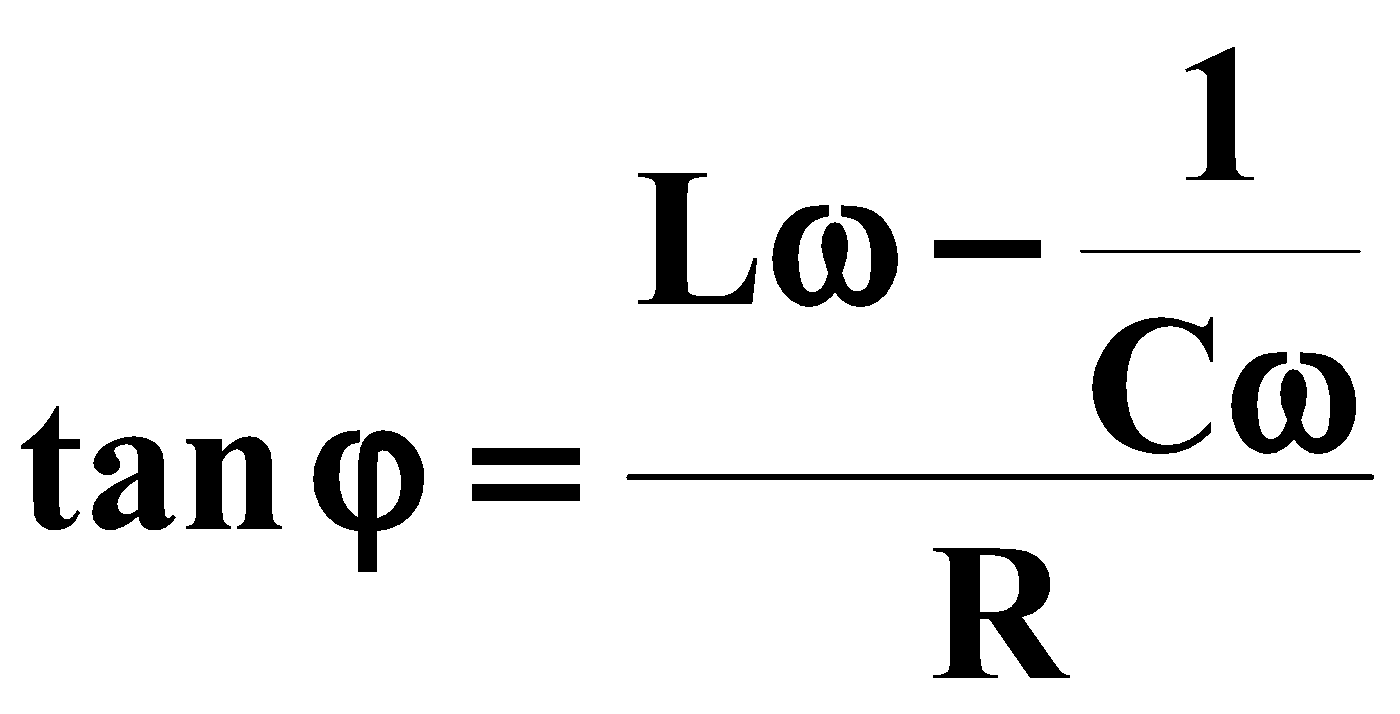
عدم الرغبة في التحميل واختلاف الصفحة :
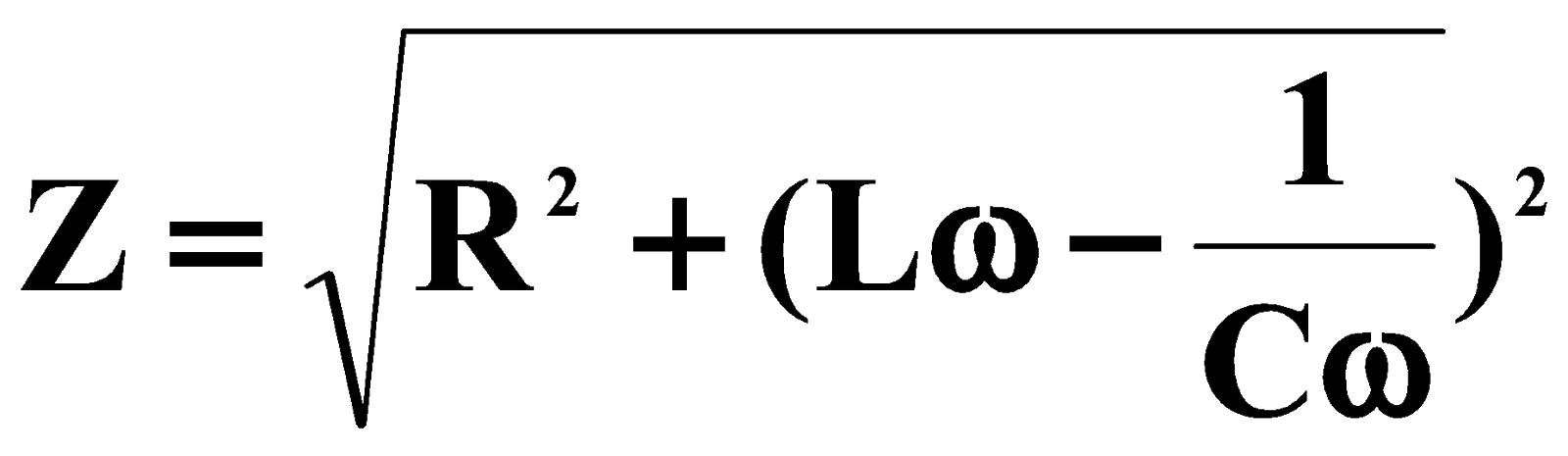
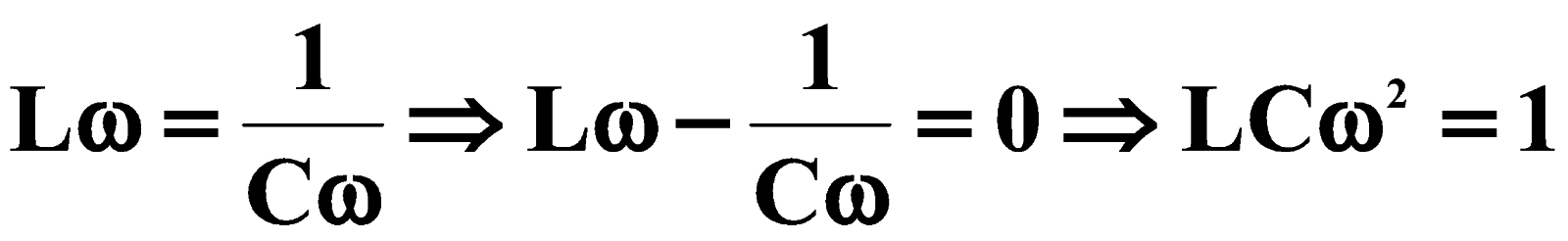
* ميزات سريعة الاستجابة :
عندما ترد علينا:
يمكننا أيضا الحصول عليها :
– استقرار التردد F والذاتية استبدل L والسعة C.
– استقرار التردد F السعة C والتغيير الذاتي L.
– تثبيت السعة C والذات L وتغيير التردد f أو النبض ω.

– دارة RLC هي تماثل دارة تحتوي على مقاومة R.
كثافة التيار القصوى.
φ = 0 – إزاحة الصفحة لـ u و i تساوي صفرًا
للاتفاق على الصفحة.
– بهيجةج وأنت أيضاإل اقلب الصفحه
أي اختلاف في الصفحة بينهما يساوي

أنا = و (ω) ، φ = و (ω
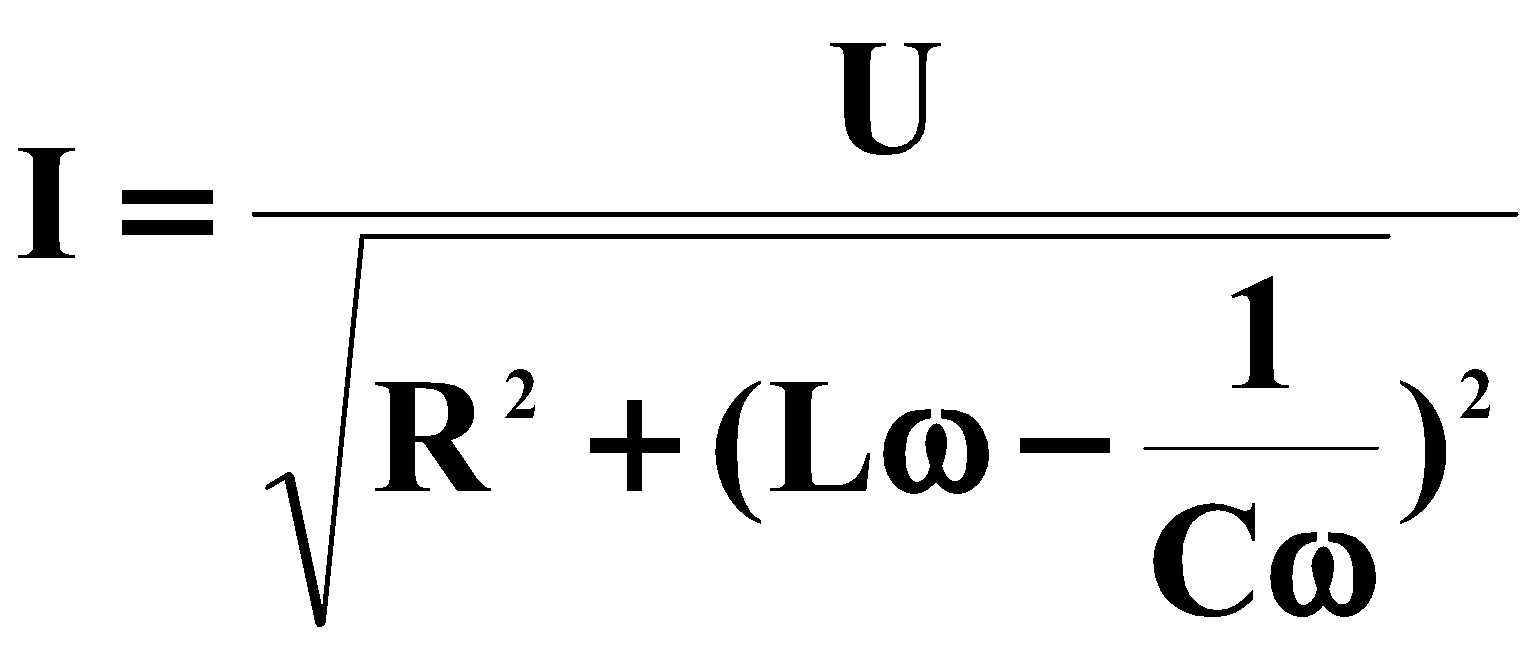
League of Transits (نطاق العبور):
* دائرة RLC :
أنا = أناإل + أنار + أناج
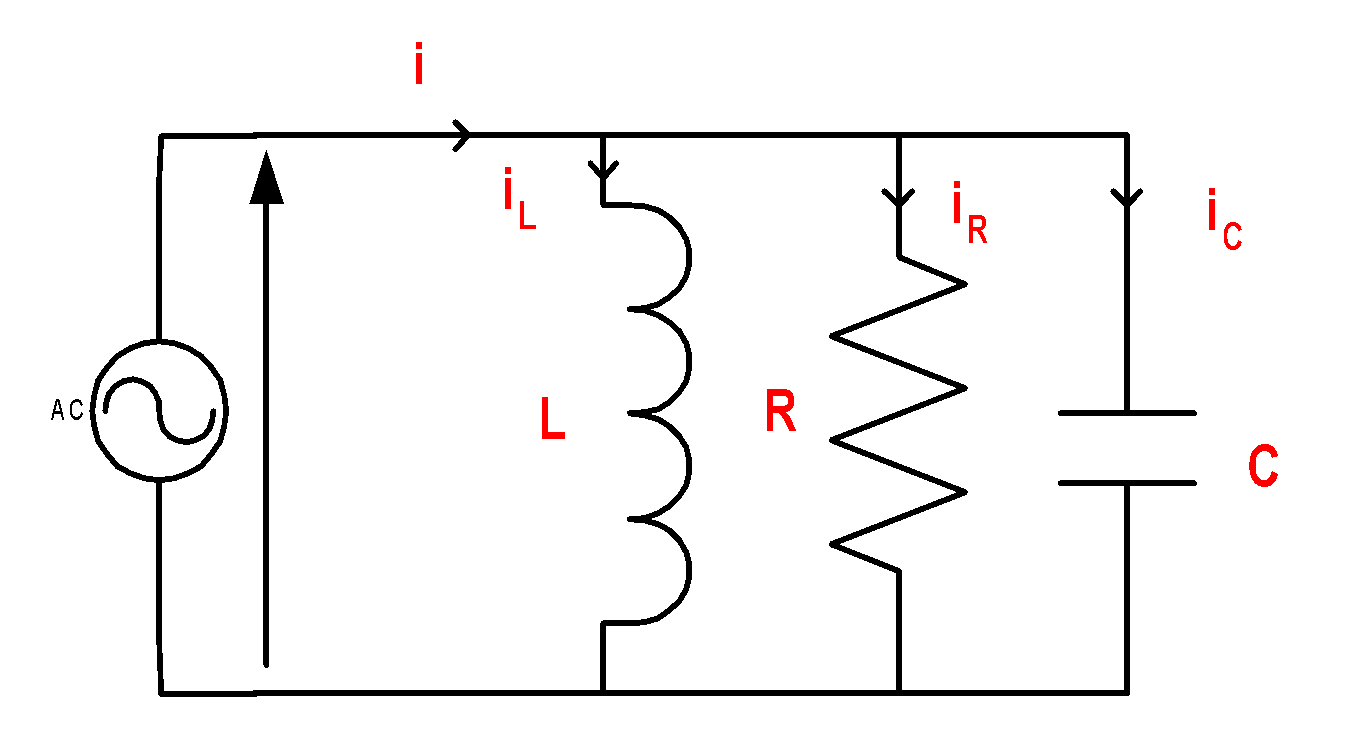
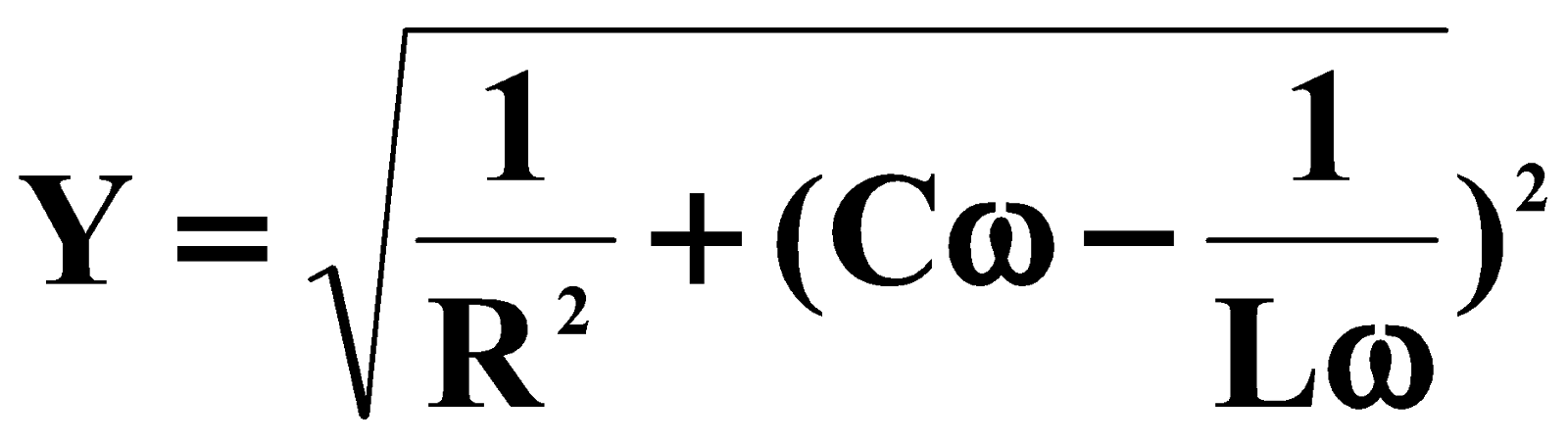
بيان الغفران:

4– الطاقة في التيار المتردد الجيبي:
1-4 قوة فورية:
نحن نعلم القوة اللحظية في المنتج: p = ui ووحدة واط (W)
4-2 القدرة الفعالة:
متوسط ذات قيمة ووحدة القدرة اللحظية هو واط (W)
– إذا كان ثنائي القطب جهاز استقبال (دعنا نقول محركًا) ، فلدينا: P> 0 cosφ> 0-/ 2 <<+ / 2.
– إذا كان ثنائي القطب مولدًا (مولد التيار المتردد): P <0 cos = "" nbsp = "" span = "">
أن تعي : cosφ يمثل عامل القدرة.
مثال: دارة بها المقاوم R: UI مع φ = 0 ⇐ cosφ = 1 P = U = RI ⇐ P = RI موجودالثاني
المقاومة تستهلك طاقة كهربائية طوال الوقت.
4-3 القوة الظاهرة : المعروف باسم صرخة الرعب
وحدتها هي Volt Amperes (VA) وتميز بعضها.
آلات الجيب مثل المحولات والمولدات.
4-4 قوة جلخ أو رجعية:: معروف بوجوده
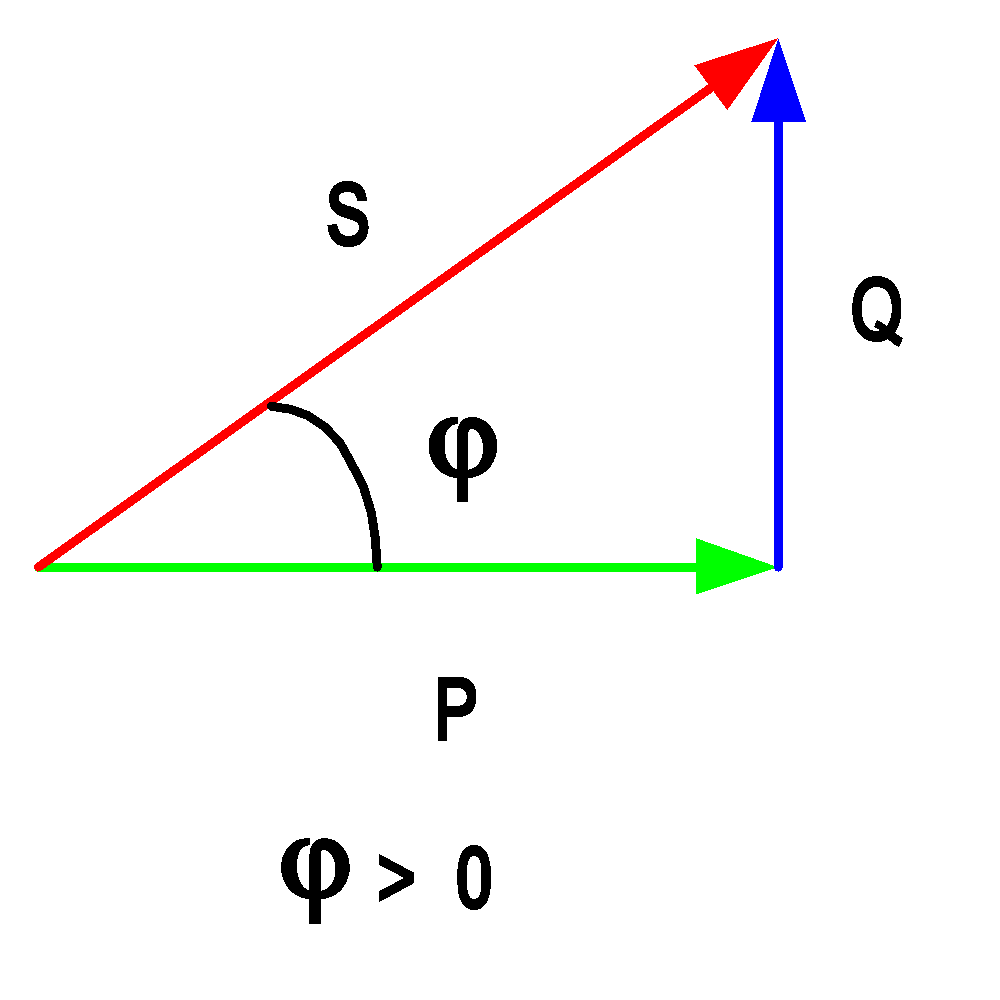
مثال ثنائي القطب عبارة عن دائرة RLC متسلسلة:
عناصر | القدرة الفعالة P (واط) | Red Power Q (متغير) | ملاحظات |
ر | ريالثاني | 0 | R يستهلك طاقة فعالة |
إل | 0 | أناالثاني | L الأحمر هو استهلاك الطاقة |
ج | 0 | 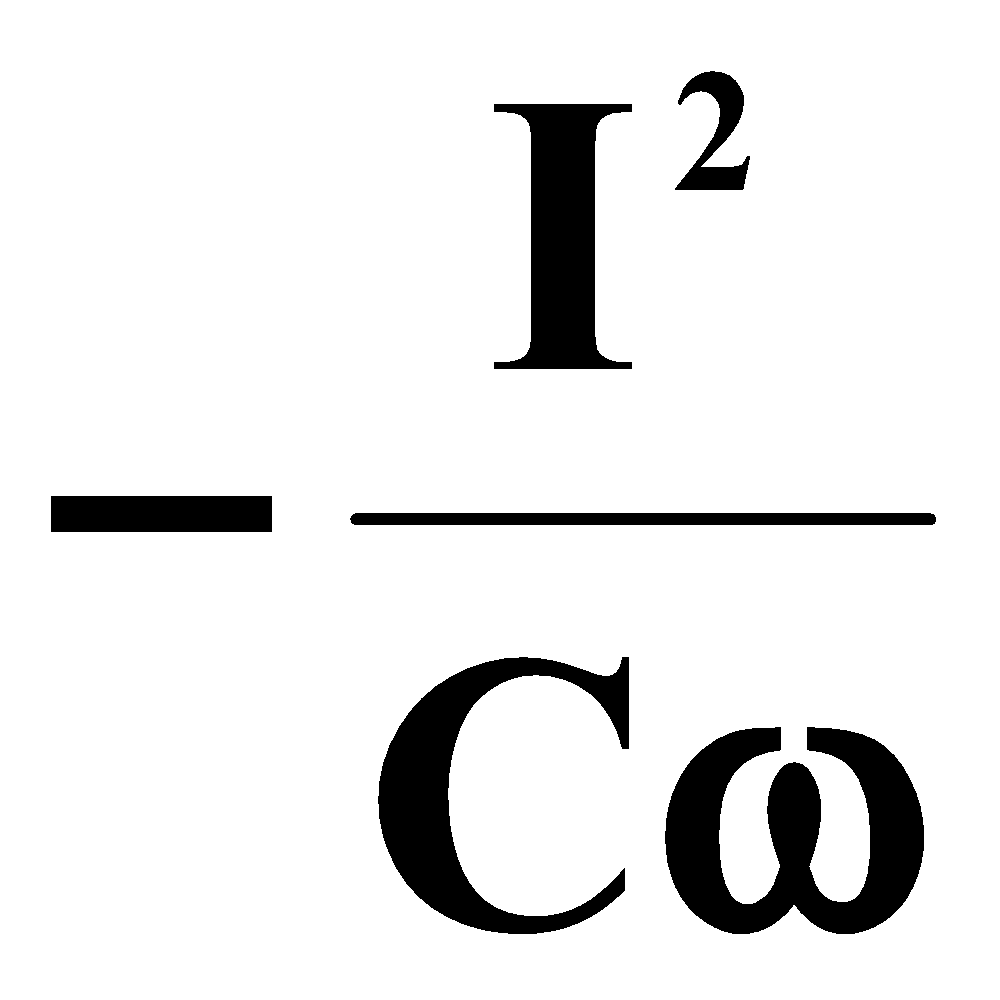 | يولد C قوة حمراء |
6- نظرية بشرو:
أ– النص النظري : في دائرة كهربائية تحتوي على أجهزة استقبال (أجهزة) تمر من خلالها التيارات الجيبية.
مجموع الطاقة الفعالة المستهلكة يساوي المجموع الجبري للطاقة الفعالة التي يستهلكها كل جهاز.
مجموع الطاقة الاحتياطية يساوي المجموع الجبري للطاقة الاحتياطية التي يستهلكها كل جهاز. لذلك نقول إنها حماية القدرات الفعالة والحمراء.
ب- طريقة بوشرو تسمح طريقة الحساب هذه بتطوير خرج طاقة وردي فعال يمكن أن يظهر في جدول:
المشترون | القدرة الفعالة P (واط) | Red Power Q (متغير) |
ثنائي القطب 1 | P1 | Q1 = P1 tanφواحد |
ثنائي القطب 2 | P2 | Q2 = P2 tanφالثاني |
شبكة التواصل | P = P1 + P2 | س = س 1 + س 2 |


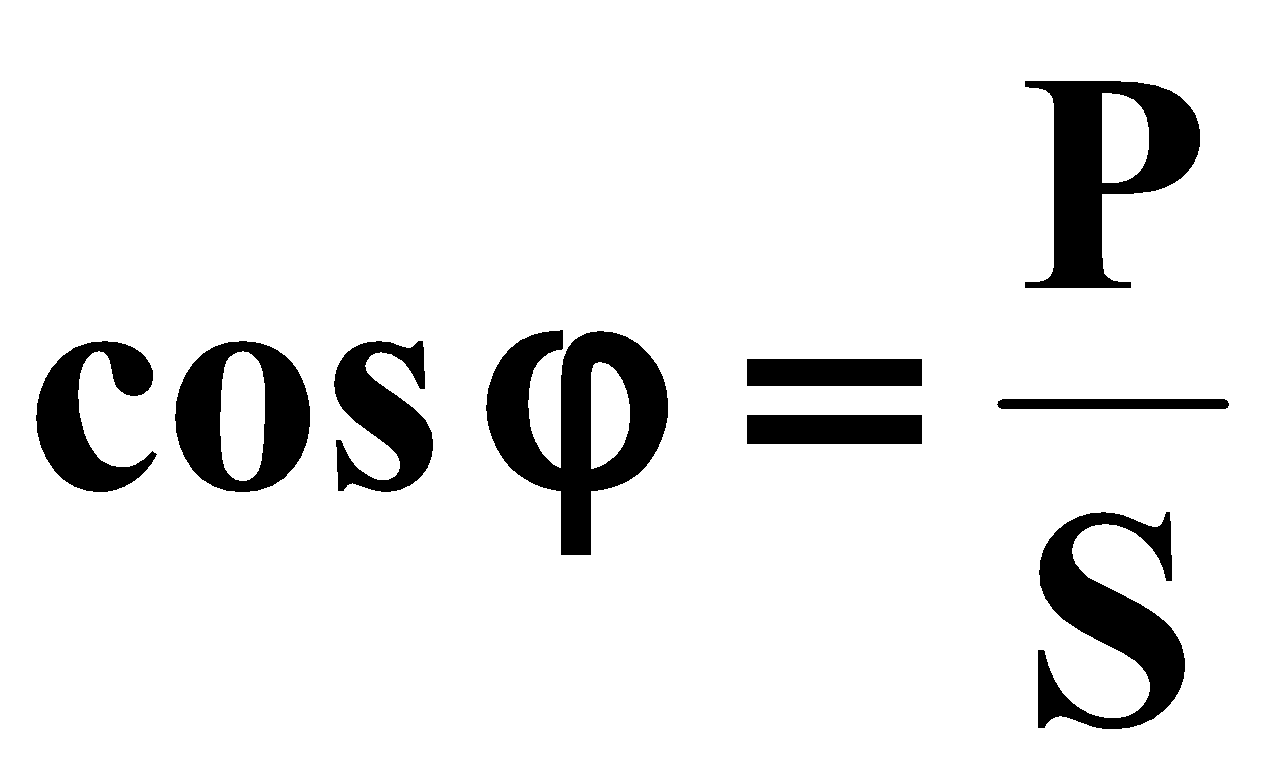
7- التيار المتردد ثلاثي الأطوار:
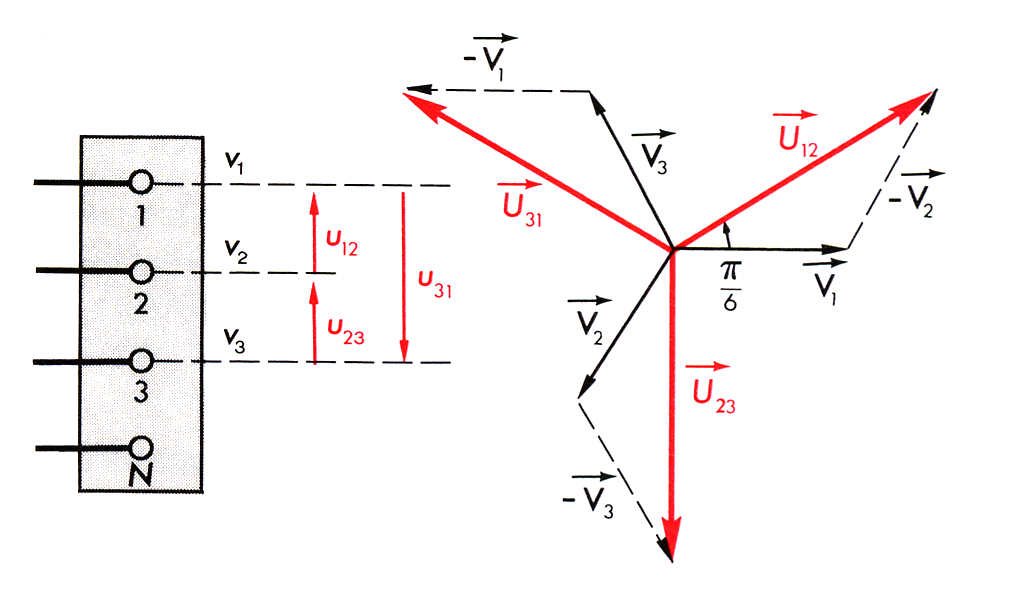
7-1 الفولتية البسيطة والمركبة:
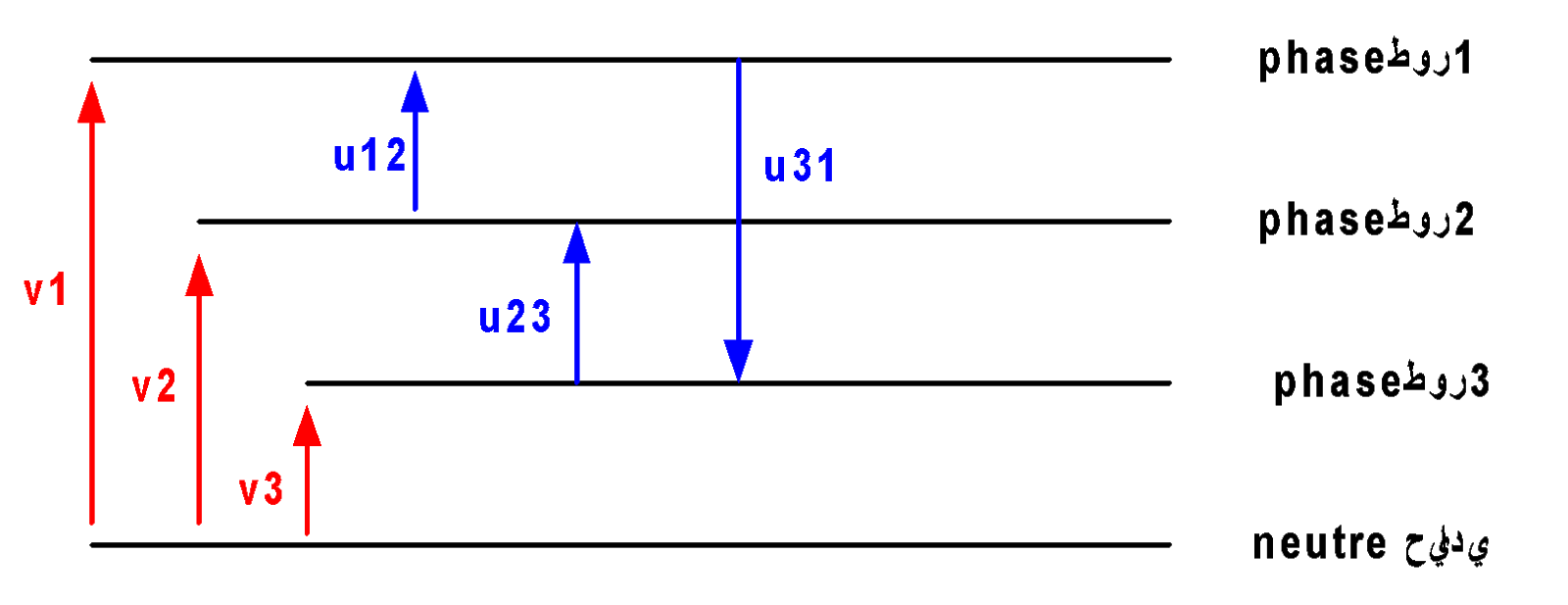
الفولتية البسيطة: v1 ، v2 ، v3 هي الفولتية الموجودة بين المرحلة المحايدة. في النموذج المتوازن:
بالنسبة لمنفذ الشبكة V1 = V2 = V3 = V = 220v.
الفولتية المركبة: u12 ، u23 ، u31 هي الفولتية الموجودة بين الطور والمرحلة. في نموذجنا المتوازن:
لدينا: u31 = v3-v1 u12 = v1-v2 ؛ u23 = v2-v3 ؛
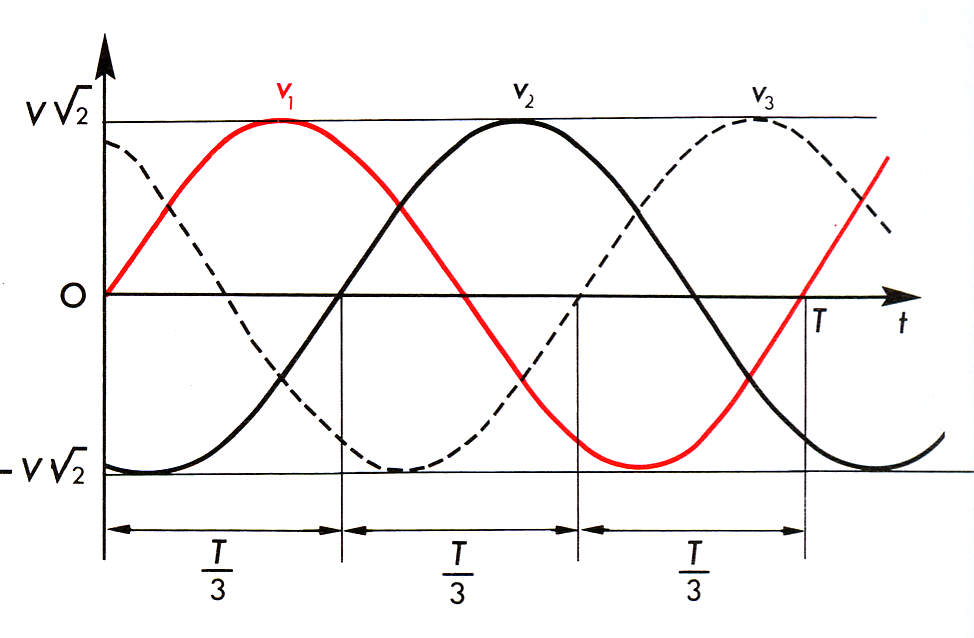
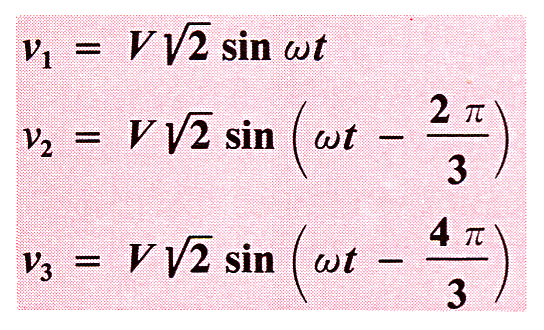
ج) – تمثيل فرينل :